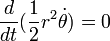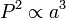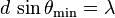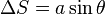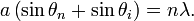Materi fisika Kelas XI semester 1 dan 2

Persamaan Gerak

Gerak Lurus Beraturan

diartikan sebagai gerakan pada lintasan lurus dengan kecepatan tetap/konstan. Kecepatan tetap berarti percepatan nol. Dengan kata lain benda yang bergerak lurus beraturan tidak memiliki percepatan. Dalam kehidupan sehari-hari sangat jarang ditemukan benda-benda yang bergerak pada lintasan lurus dengan kecepatan tetap.

Karena pada Gerak Lurus Beraturan (GLB) kecepatan gerak suatu benda tetap, maka kecepatan rata-rata sama dengan kecepatan atau kelajuan sesaat.

GRAFIK GERAK LURUS BERATURAN (GLB)

Grafik Kecepatan terhadap Waktu (v-t)

Berdasarkan grafik di atas, tampak bahwa kecepatan bernilai tetap pada tiap satuan waktu. Kecepatan tetap ditandai oleh garis lurus, berawal dari t = 0 hingga t akhir.

Contoh : perhatikan grafik kecepatan terhadap waktu (v-t) di bawah ini

Kecepatan gerak benda pada grafik di atas adalah 3 m/s. 1, 2, 3 dstnya adalah waktu tempuh (satuannya detik). Amati bahwa walaupun waktu berubah dari 1 detik sampai 5, kecepatan benda selalu sama (ditandai oleh garis lurus).

Bagaimana kita mengetahui perpindahan benda melalui grafik di atas ? luas daerah yang diarsir pada grafik di atas sama dengan perpindahan benda. Jadi, untuk mengetahui besarnya perpindahan, hitung saja luas daerah yang diarsir. Tentu saja satuan perpindahan adalah satuan panjang, bukan satuan luas.

Dari grafik di atas, v = 5 m/s, sedangkan t = 3 s. Dengan demikian, jarak yang ditempuh benda = (5 m/s x 3 s) = 15 m. Cara lain menghitung jarak tempuh adalah dengan menggunakan persamaan GLB. s = v t = 5 m/s x 3 s = 15 m.

Persamaan GLB yang kita gunakan untuk menghitung jarak atau perpindahan di atas berlaku jika gerak benda memenuhi grafik tersebut. Pada grafik terlihat bahwa pada saat t = 0 s, maka v = 0. Artinya, pada mulanya benda diam, baru kemudian bergerak dengan kecepatan 5 m/s. Padahal dapat saja terjadi bahwa saat awal kita amati benda sudah dalam keadaan bergerak, sehingga benda telah memiliki posisi awal s₀. Untuk itu lebih memahami hal ini, pelajari grafik di bawah ini.

Grafik Kedudukan terhadap Waktu (x-t)

Grafik kedudukan terhadap waktu, di mana kedudukan awal x₀ berhimpit dengan titik acuan nol.

Makna grafik di atas adalah bahwa nilai kecepatan selalu tetap pada setiap titik lintasan (diwakili oleh titik-titik sepanjang garis x pada sumbu y) dan setiap satuan waktu (diwakili setiap titik sepanjang t pada sumbu x). Anda jangan bingung dengan kemiringan garis yang mewakili kecepatan. Makin besar nilai x, makin besar juga nilai t sehingga hasil perbandingan x dan y (kecepatan) selalu sama.

Contoh : Perhatikan contoh Grafik Kedudukan terhadap Waktu (x-t) di bawah ini

Bagaimanakah cara membaca grafik ini ?

Pada saat t = 0 s, jarak yang ditempuh oleh benda x = 0, pada saat t = 1 s, jarak yang ditempuh oleh benda = 2 m, pada saat t = 2 s jarak yang ditempuh oleh benda = 4 m, pada saat t = 3 s, jarak yang ditempuh oleh benda = 6 s dan seterusnya. Berdasarkan hal ini dapat kita simpulkan bahwa gerak benda yang diwakili oleh grafik x- t di atas, bergerak dengan kecepatan tetap 2 m/s (Ingat, kecepatan adalah jarak dibagi waktu).

Grafik kedudukan terhadap waktu, di mana kedudukan awal x₀ tidak berhimpit dengan titik acuan nol.

Persamaan yang kita turunkan di atas menjelaskan hubungan antara kedudukan suatu benda terhadap fungsi waktu, di mana kedudukan awal benda tidak berada pada titik acuan nol. Kecepatan benda diawali dari kedudukan di x₀ sehingga besar x₀ harus ditambahkan dalam perhitungan. Pada grafik di atas x_o = 0.

(pahami secara perlahan-lahan penurunan rumus di atas, bila perlu sambil melihat grafik untuk mempermudah pemahaman anda)

Latihan soal

Kereta api Ladoya bergerak lurus beraturan pada rel lurus yogya-bandung sejauh 5 km dalam selang waktu 5 menit. (a) Hitunglah kecepatan kereta (b) berapa lama kereta itu menempuh jarak 50 km ?

Panduan Jawaban :

(a) Pada soal di atas, diketahui perpindahan (s) = 5 km dan waktu tempuh (t) = 4 menit. Sebelum menghitung kecepatan, kita harus mengkonversi satuan sehingga sesuai dengan Sistem Internasional (SI). Terserah anda, mana yang ingin dikonversi, ubah menit ke jam atau km di ubah ke meter dan menit di ubah ke detik.

Misalnya yang di ubah adalah satuan menit, maka 4 menit = 0,07 jam.

Ingat bahwa pada GLB, kecepatan benda sama setiap saat, demikian juga dengan kecepatan rata-rata.

v = s / t = 5 km / 0,07 jam = 75 km/jam

(b) Untuk menghitung waktu, persamaan kecepatan di atas dibalik

t = s / v = 50 km / 75 km/jam = 0,67 jam = 40 menit.

Gerak Lurus Berubah Beraturan

diartikan sebagai gerak benda dalam lintasan lurus dengan percepatan tetap. Mula-mula dari keadaan diam, benda mulai bergerak, semakin lama semakin cepat dan kecepatan gerak benda tersebut berubah secara teratur. Perubahan kecepatan bisa berarti tejadi pertambahan kecepatan atau pengurangan kecepatan. Pengurangan kecepatan terjadi apabila benda akan berhenti. dalam hal ini benda mengalami perlambatan tetap. Pada pembahasan ini kita tidak menggunakan istilah perlambatan untuk benda yang mengalami pengurangan kecepatan secara teratur. Kita tetap menamakannya percepatan, hanya nilainya negatif. Jadi perlambatan sama dengan percepatan yang bernilai negatif.

Pada pembahasan mengenai percepatan, kita telah menurunkan persamaan/rumus percepatan rata-rata, di mana

t₀ adalah waktu awal ketika benda hendak bergerak, t adalah waktu akhir. Karena pada saat t₀ benda belum bergerak maka kita bisa mengatakan t₀ (waktu awal) = 0. Nah sekarang persamaan berubah menjadi :

Satu masalah umum dalam GLBB adalah menentukan kecepatan sebuah benda pada waktu tertentu, jika diketahui percepatannya (sekali lagi ingat bahwa percepatan tetap). Untuk itu, persamaan percepatan yang kita turunkan di atas dapat digunakan untuk menyatakan persamaan yang menghubungkan kecepatan pada waktu tertentu (v_t), kecepatan awal (v₀) dan percepatan (a). sekarang kita obok2 persamaan di atas…. Jika dibalik akan menjadi

ini adalah salah satu persamaan penting dalam GLBB, untuk menentukan kecepatan benda pada waktu tertentu apabila percepatannya diketahui. Jangan dihafal, pahami saja cara penurunannya dan rajin latihan soal biar semakin diingat….

Selanjutnya, mari kita kembangkan persamaan di atas (persamaan I GLBB) untuk mencari persamaan yang digunakan untuk menghitung posisi benda setelah waktu t ketika benda tersebut mengalami percepatan tetap.

Pada pembahasan mengenai kecepatan, kita telah menurunkan persamaan kecepataan rata-rata

Karena pada GLBB kecepatan rata-rata bertambah secara beraturan, maka kecepatan rata-rata akan berada di tengah-tengah antara kecepatan awal dan kecepatan akhir;

Persamaan ini berlaku untuk percepatan konstan dan tidak berlaku untuk gerak yang percepatannya tidak konstan. Kita tulis kembali persamaan a :

Persamaan ini digunakan untuk menentukan posisi suatu benda yang bergerak dengan percepatan tetap. Jika benda mulai bergerak pada titik acuan = 0 (atau x₀ = 0), maka persamaan II dapat ditulis menjadi

Sekarang kita turunkan persamaan/rumus yang dapat digunakan apabila t (waktu) tidak diketahui.

Sekarang kita subtitusikan persamaan ini dengan nilai t pada persamaan c

Terdapat empat persamaan yang menghubungkan posisi, kecepatan, percepatan dan waktu, jika percepatan (a) konstan, antara lain :

Persamaan di atas tidak berlaku jika percepatan tidak konstan/tetap. Ingat bahwa x menyatakan posisi/kedudukan, bukan jarak dan ( x – x₀ ) adalah perpindahan (s)

Latihan Soal

1. Sebuah mobil sedang bergerak dengan kecepatan 20 m/s ke utara mengalami percepatan tetap 4 m/s² selama 2,5 sekon. Tentukan kecepatan akhirnya

Panduan jawaban :

Pada soal, yang diketahui adalah kecepatan awal (v₀) = 20 m/s, percepatan (a) = 4 m/s dan waktu tempuh (t) = 2,5 sekon. Karena yang diketahui adalah kecepatan awal, percepatan dan waktu tempuh dan yang ditanyakan adalah kecepatan akhir, maka kita menggunakan persamaan/rumus

Gerak Melingkar

Gerak Melingkar Beraturan

kecepatan pada GMB selalu berubah (ingat perbedaan antara kelajuan dan kecepatan, kelajuan adalah besaran skalar sedangkan kecepatan adalah besaran vektor yang memiliki besar/nilai dan arah) sehingga kita tidak dapat mengatakan kecepatan linear pada GMB tetap.

Pada gerak melingkar beraturan, besar kecepatan linear v tetap, karenanya besar kecepatan sudut juga tetap.

Jika arah kecepatan linear alias kecepatan tangensial selalu berubah, bagaimana dengan arah kecepatan sudut ? arah kecepatan sudut sama dengan arah putaran partikel, untuk contoh di atas arah kecepatan sudut searah dengan arah putaran jarum jam. Karena besar maupun arah kecepatan sudut tetap maka besaran vektor yang tetap pada GMB adalah kecepatan sudut. Dengan demikian, kita bisa menyatakan bahwa GMB merupakan gerak benda yang memiliki kecepatan sudut tetap.

Pada GMB, kecepatan sudut selalu tetap (baik besar maupun arahnya). Karena kecepatan sudut tetap, maka perubahan kecepatan sudut atau percepatan sudut bernilai nol. Percepatan sudut memiliki hubungan dengan percepatan tangensial, sesuai dengan persamaan

Karena percepatan sudut dalam GMB bernilai nol, maka percepatan linear juga bernilai nol. Jika demikian, apakah tidak ada percepatan dalam Gerak Melingkar Beraturan (GMB) ?

Pada GMB tidak ada komponen percepatan linear terhadap lintasan, karena jika ada maka lajunya akan berubah. Karena percepatan linear alias tangensial memiliki hubungan dengan percepatan sudut, maka percepatan sudut juga tidak ada dalam GMB. Yang ada hanya percepatan yang tegak lurus terhadap lintasan, yang menyebabkan arah kecepatan linear berubah-ubah. Sekarang mari kita tinjau percepatan ini.

PERCEPATAN SENTRIPETAL

Percepatan tangensial didefinisikan sebagai perbandingan perubahan kecepatan dengan selang waktu yang sangat singkat, secara matematis dirumuskan sebagai berikut :

Sekarang kita turunkan persamaan untuk menentukan besar percepatan sentripetal alias percepatan radial (a_R)

Kita tulis semua kecepatan dengan v karena pada GMB kecepatan tangensial benda sama (v₁ = v₂ = v).

Benda yang melakukan gerakan dengan lintasan berbentuk lingkaran dengan jari-jari (r) dan laju tangensial tetap (v) mempunyai percepatan yang arahnya menuju pusat lingkaran dan besarnya adalah :

Berdasarkan persamaan percepatan sentripetal tersebut, terlihat bahwa nilai percepatan sentripetal bergantung pada kecepatan tangensial dan radius/jari-jari lintasan (lingkaran). Dengan demikian, semakin cepat laju gerakan melingkar, semakin cepat terjadi perubahan arah dan semakin besar radius, semakin lambat terjadi perubahan arah.

Arah vektor percepatan sentripetal selalu menuju ke pusat lingkaran, tetapi vektor kecepatan linear menuju arah gerak benda secara alami (lurus), sedangkan arah kecepatan sudut searah dengan putaran benda. Dengan demikian, vektor percepatan sentripetal dan kecepatan tangensial saling tegak lurus atau dengan kata lain pada Gerak Melingkar Beraturan arah percepatan dan kecepatan linear/tangensial tidak sama. Demikian juga arah percepatan sentripetal dan kecepatan sudut tidak sama karena arah percepatan sentripetal selalu menuju ke dalam/pusat lingkaran sedangkan arah kecepatan sudut sesuai dengan arah putaran benda (untuk kasus di atas searah dengan putaran jarum jam).

Kita dapat menyimpulkan bahwa dalam Gerak Melingkar Beraturan :

1. besar kecepatan linear/kecepatan tangensial adalah tetap, tetapi arah kecepatan linear selalu berubah setiap saat
2. kecepatan sudut (baik besar maupun arah) selalu tetap setiap saat
3. percepatan sudut maupun percepatan tangensial bernilai nol
4. dalam GMB hanya ada percepatan sentripetal

Gerak Melingkar Berubah Beraturan

Adalah gerak suatu benda dengan bentuk lintasan melingkar dan besar percepatan sudut/anguler (α) konstan.
Jika perecepatan anguler benda searah dengan perubahan kecepatan anguler maka perputaran benda semakin cepat, dan dikatakan GMBB dipercepat. Sebaliknya jika percepatan anguler berlawanan arah dengan perubahan kecepatan anguler benda akan semakin lambat, dan dikatakan GMBB diperlambat.

1. Percepatan Anguler (α)

Sebuah benda bergerak melingkar dengan laju anguler berubah beraturan memiliki perubahan kecepatan angulernya adalah :

Δω = ω₂ – ω₁

Dan perubahan waktu kecepatan anguler adalah Δt, maka di dapatkan :

∆ω = perubahan kecepatan sudut (rad/s)
∆t = selang waktu (s)
α = percepatan sudut/anguler (rads^-2)

Sama halnya dengan Gerak Lurus Berubah Beraturan (GLBB), pada GMBB berlaku juga :

- Mencari kecepatan sudut akhir (ω_t) :

ω_t = ω₀ ± α.t

- Mencari posisi sudut / besar sudut (θ) yang ditempuh:

θ= ω₀ t ± α.t²

x = R. θ

Dapat diperoleh juga :

ωt² = ω₀² ± 2 α.θ

dimana :

ωt = kecepatan sudut/anguler keadaan akhir(rad/s)
ω0 = kecepatan sudut/anguler keadaan awal (rad/s)
θ = besar sudut yang ditempuh (radian, putaran)
1 rpm = 1 putaran permenit
1 putaran = 360° = 2p rad.
x = perpindahan linier (m)
t = waktu yang diperlukan (s)
R = jari-jari lintasan (m)

2. Percepatan Tangensial (at)

Pada gerak melingkar berubah beraturan selain percepatan sentripetal (as) juga mempunyai percepatan tangensial (at).

Percepatan Tangensial (at) diperoleh :

maka : a_t = . R dengan arah menyinggung lintasan.

Partikel P memiliki komponen Percepatan :

a = a_t + a_s , dimana a_t tegak lurus a_s ( a_s a_t )

Besar Percepatan Linier Total partikel titik P :

a_t = percepatan tangensial (ms^-2)
a_s = percepatan sentripetal (ms^-2)
a = percepatan total (ms^-2)

Jika a_s = dan maka didapat :

Percepatan total (a) :

dimana

V = kelajuan linier (m/s)
R = jari-jari lintasan (m)
= percepatan sudut (rad s^-2)

Semua benda bergerak melingkar selalu memiliki percepatan sentripetal, tetapi belum tentu memiliki percepatan tangensial.

Percepatan tangensial hanya dimiliki bila benda bergerak melingkar dan mengalami perubahan kelajuan linier.

Benda yang bergerak melingkar dengan kelajuan linier tetap hanya memiliki percepatan sentripetal, tetapi tidak mempunyai percepatan tangensial (a_t = 0 ).

Contoh soal Konsep Gerak Melingkar Berubah Beraturan:
Sebuah roda mobil sedang berputar dengan kecepatan sudut 8,6 rad/s. Suatu gesekan kecil pada poros putaran menyebabkan suatu perlambatan sudut tetap sehingga akhirnya berhenti dalam waktu 192 s. Tentukan :

1. Percepatan sudut
2. Jarak yang telah ditempuh roda dari mulai bergerak sampai berhenti (jari-jari roda 20 cm)

Pembahasan :

Diketahui : ω₀= 8,6 rad/s

ω_t = 0 rad/s

t = 192 s
R = 10cm= 0,1 m

Ditanya : a.
b. x

Jawab :

a.

= - 0,045 rads^-2

b.

= (8,6).(192) + (-0,045).(192)²

= 826 rad

x = R.θ

= (0,1m),(826)

= 82,6 m

Gerak Parabola

ila suatu benda bergerak dengan litasan berbentuk parabola, maka benda tersebut dinamakan gerak parabola. Benda A bergerak dari arah kiri mengikuti gerakan parabolik maka panjang lintasannya dipengaruhi oleh besarnya sudut ketika pertama kali dia melintas.

Gerak ini terdiri dari dua jenis, yaitu:

1. Gerak Setengah Parabola

Benda yang dilempar mendatar dari suatu ketinggian tertentu dianggap tersusun atas dua macam gerak, yaitu :

a.	Gerak pada arah sumbu X (GLB) vx = v0 Sx = X = vx t

b.

Gerak pada arah sumbu Y (GJB/GLBB)

v_y = 0
]® Jatuh bebas
y = 1/2 g t²

2. Gerak Parabola/Peluru

Benda yang dilempar ke atas dengan sudut tertentu, juga tersusun atas dua macam gerak dimana lintasan
dan kecepatan benda harus diuraikan pada arah X dan Y.

a.	Arah sb-X (GLB) v0x = v0 cos q (tetap) X = v0x t = v0 cos q.t

b.	Arah sb-Y (GLBB) v0y = v0 sin q Y = voy t - 1/2 g t2 = v0 sin q . t - 1/2 g t2 vy = v0 sin q - g t

Syarat mencapai titik P (titik tertinggi): v_y = 0

t_op = v₀ sin q / g

sehingga

t_op = t_pq
t_oq = 2 t_op

OQ = v_0x t_Q = V₀² sin 2q / g

h _max = v _oy t_p - 1/2 gt_p² = V₀² sin² q / 2g

vt = Ö (vx)² + (vy)²

Contoh:

1. Sebuah benda dijatuhkan dari pesawat terbang yang sedang melaju horisontal 720 km/jam dari ketinggian 490 meter. Hitunglah jarak jatuhnya benda pada arah horisontal ! (g = 9.8 m/det²).

Jawab:

v_x = 720 km/jam = 200 m/det.
h = 1/2 gt² ® 490 = 1/2 . 9.8 . t²
t = 100 = 10 detik
X = v_x . t = 200.10 = 2000 meter

Gaya

Gaya Berat

Berat suatu benda adalah massa suatu benda yang dipengaruhi oleh percepatan gravitasi bumi, di tempat yang gravitasinya berbeda berat benda akan berubah.

Berdasarkan Hukum II Newton, berat benda dirumuskan:

w = m.g

di mana

w = m = g =

gaya gravitasi bumi pada benda atau berat benda dalamNewton massa benda, dalam kg percepatan gravitasi bumi yang besarnya 9,8 ms-2 kadang-kadang untuk memudahkan dibulatkan menjadi 10 ms-2

Contoh

Berat benda yang massanya 2 kg, jika g = 9,8 ms^-2 adalah:

w = w = w =

m g 2. 9,8 19,6 Newton.

Makin jauh dari bumi percepatan gravitasi bumi makin kecil, sehingga berat roket pada saat di A lebih besar dibandingkan roket di B.

Gambar 2.5. Roket di atas Bumi.

Semua benda yang berada di atas permukaan bumi pada jarak tertentu dari pusat bumi akan mengalami gaya gravitasi yang dinamakan gaya berat w. Gaya berat w kedudukannya pada pusat massa benda itu dan arahnya menuju pusat bumi. Beberapa gambar gaya berat benda diperlihatkan oleh gambar 2.6.

Gambar 2.6. Kedudukan Gaya Berat.

Dari gambar 2.6. nampak bahwa gaya berat (w) dapat digambarkan mengambil kedudukan tegak lurus terhadap permukaan tanah.

Dalam menyelesaikan persoalan-persoalan dinamika penempatan gaya berat dan gaya normal dalam sistem benda turut menentukan hasil yang diperoleh.

Gaya Normal

Ketika kita meletakan sebuah kotak di atas meja, berat kotak tersebut menekan meja ke bawah dan sebaliknya meja membalas dengan memberikan gaya ke atas (lihat gambar di bawah). Gaya yang diberikan oleh meja bisa disebut gaya kontak, karena gaya tersebut terjadi karena adanya sentuhan antara kotak dan meja. Sebuah gaya kontak yang tegak lurus terhadap permukaan kontak disebut Gaya Normal (normal berarti tegak lurus), dan mempunyai Lambang F_N atau bisa ditulis N.

Kedua gaya yang ditunjukkan pada gambar diatas bekerja pada kotak sehingga kotak tetap diam. Selisih kedua gaya tersebut (gaya total) pasti nol, sehinga kotak tersebut diam/tidak jatuh ke tanah. F_G atau w dan N pasti memiliki besar yang sama dan memiliki arah yang berlawanan, sehingga gaya total atau selisih kedua gaya tersebut nol. Gaya-gaya tersebut bukan gaya aksi reaksi yang dijelaskan pada Hukum III Newton. Ingat bahwa gaya aksi reaksi bekerja pada benda yang berbeda, sedangkan kedua gaya di atas (Gaya berat dan Gaya Normal) bekerja pada benda yang sama, yakni kotak. Perhatikan gambar di atas secara seksama. Gaya berat benda yang menekan meja digambarkan pada titik pusat kotak alias berada di tengah-tengah kotak. Sedangkan Gaya Normal digambarkan pada permukaan sentuh antara kotak dan meja.

Lalu apa gaya reaksinya ? gaya ke atas yang diberikan oleh meja terhadap kotak adalah N, disebut gaya aksi. Gaya reaksi diberikan oleh kotak kepada meja, yakni N’, sebagaimana diperlihatkan pada gambar di bawah. Perhatikan baik-baik posisi tanda panah pada gambar. Tanda panah yang mewakili N’ digambarkan pada meja, bukan pada kotak. Panjang tanda panah sama, hal ini menunjukkan bahwa besarnya gaya sama, hanya berlawanan arah (aksi = - reaksi). Mengenai aksi-reaksi selengkapnya dipelajari pada Pokok Bahasan Hukum III Newton.

Gaya Normal (N) bekerja pada bidang sentuh antara dua benda yang saling bersentuhan dan arahnya selalu tegak lurus pada bidang sentuh. Beberapa contoh arah Gaya Normal terhadap gaya sentuh ditunjukkan pada gambar di bawah.

Gaya Tegang Tali

• Gaya tegang tali adalah gaya yang terjadi pada tali, pegas atau batang yang ujung-ujung dihubungkan dengan bendalain.

• Gaya tegang tali memenuhi:

T =∑ F = mg

Gaya Gesek

Gaya gesek adalah gaya yang menahan gerak benda agar benda itu dapat berhenti bergerak.
Besar kecilnya gaya gesek dipengaruhi oleh kasar licinnya permukaan benda yang bergesekan.
Makin halus/licin permukaan gaya gesek semakin kecil.
Makin kasar permukaan gaya gesek semakin besar.

Gaya Gesek Statis

Gaya gesekan yang bekerja pada dua permukaan benda yang bersentuhan, ketika benda tersebut belum bergerak disebut gaya gesek statik (lambangnya f_s). Gaya gesek statis yang maksimum sama dengan gaya terkecil yang dibutuhkan agar benda mulai bergerak. Ketika benda telah bergerak, gaya gesekan antara dua permukaan biasanya berkurang sehingga diperlukan gaya yang lebih kecil agar benda bergerak dengan laju tetap. Ketika benda telah bergerak, gaya gesekan masih bekerja pada permukaan benda yang bersentuhan tersebut.

KOOFISIEN GESEKAN STATIK DAN KINETIK

hubungan antara gaya normal dan gaya gesekan pada persamaan di atas hanya untuk besarnya saja. Arah kedua gaya tersebut selalu saling tegak lurus satu dengan yang lain, sebagaimana diperlihatkan pada gambar di bawah ini. Berikut ini keterangan untuk gambar di bawah : f_k adalah gaya gesekan kinetik, f_s adalah gaya gesekan statik, F adalah gaya tarik, N adalah gaya normal, w adalah gaya berat, m adalah massa, g adalah percepatan gravitasi.

Gaya Gesek Kinetis

etika benda telah bergerak, gaya gesekan masih bekerja pada permukaan benda yang bersentuhan tersebut. Gaya gesekan yang bekerja ketika benda bergerak disebut gaya gesekan kinetik (lambangnya f_k) (kinetik berasal dari bahasa yunani yang berarti “bergerak”). Ketika sebuah benda bergerak pada permukaan benda lain, gaya gesekan bekerja berlawanan arah terhadap kecepatan benda. Hasil eksperimen menunjukkan bahwa pada permukaan benda yang kering tanpa pelumas, besar gaya gesekan sebanding dengan Gaya Normal.

Contoh Soal :

Sebuah balok bermassa 10 kg diletakkan pada bidang miring sebagaimana tampak pada gambar di bawah. Jika sudut yang dibentuk antara bidang miring dengan permukaan lantai sebesar 30^o dan koofisien gesekan kinetik adalah 0,4, berapakah gaya gesekan kinetis yang bekerja pada permukaan balok dan bidang miring ?

Jawaban

Gaya Gravitasi

Gravitasi adalah gaya tarik menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta. Fisika modern mendeskripsikan gravitasi menggunakan. teori relativitas umum dari Einstein, namun hukum gravitasi universal newton yang lebih sederhana merupakan hampiran yang cukup akurat dalam kebanyakan kasus.

Sebagai contoh,bumi yang memiliki massa yang sangat besar menghasilkan gaya gravitasi yang sangat besar untuk menarik benda-benda di sekitarnya, termasuk makhluk hidup dan benda-benda yang ada di bumi. Gaya gravitasi ini juga menarik benda-benda yang ada diluar angkasa, seperti bulan , meteor, dan benda angkasa lainnya, termasuk satelit buatan manusia.

Hukum gravitasi universal Newton dirumuskan sebagai berikut:

Setiap massa titik menarik semua massa titik lainnya dengan gaya segaris dengan garis yang menghubungkan kedua titik. Besar gaya tersebut berbanding lurus dengan perkalian kedua massa tersebut dan berbanding terbalik dengan kuadrat jarak antara kedua massa titik tersebut.

F adalah besar dari gaya gravitasi antara kedua massa titik tersebut

G adalah konstanta gravitasi

m₁ adalah besar massa titik pertama

m₂ adalah besar massa titik kedua

r adalah jarak antara kedua massa titik, dan

g adalah percepatan gravitasi =

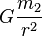
Dalam sistem internasional, F diukur dalam newton (N), m₁ dan m₂ dalam kilogram (kg), r dalam meter (m), dsn konstanta G kira-kira sama dengan 6,67 × 10⁻¹¹ N m² kg⁻².

Dari persamaan ini dapat diturunkan persamaan untuk menghitung berat. Berat suatu benda adalah hasil kali massa benda tersebut dengan percepatan gravitasi bumi Persamaan tersebut dapat dituliskan sebagai berikut: W = mg. W adalah gaya berat benda tersebut, m adalah massa dan g adalah percepatan gravitasi. Percepatan gravitasi ini berbeda-beda dari satu tempat ke tempat lain Gaya Pegas

1. Elastisitas dan Hukum Hooke

   Bila suatu benda dikenai sebuah gaya dan kemudian gaya tersebut dihilangkan, maka benda akan kembali ke bentuk semula, berarti benda itu adalah benda elastis. Namun pada umumnya benda bila dikenai gaya tidak dapat kembali ke bentuk semula walaupun gaya yang bekerja sudah hilang. Benda seperti ini disebut benda plastis. Contoh benda elastis adalah karet ataupun pegas. Bila pegas ditarik melebihi batasn tertentu maka benda itu tidak akan elastis lagi. Lalu bagaimanakah hubungan pertambahan panjang dengan gaya tarik?

   Karena besarnya gaya pemulih sebanding besarnya pertambahan panjang, maka dapat dirumuskan bahwa:
   

   
   
   dengan,
   k = konstanta pegas
   F_p = Gaya Pemulih (N)
   x = Perpanjangan Pegas (m) Persamaan inilah yang disebut dengan Hukum Hooke. Tanda negatif (-) dalam persamaan menunjukkan berarti gaya pemulih berlawanan arah dengan arah perpanjangan.
2. Modulus Elastisitas

   Yang dimaksud dengan Mosdulus Elastisitas adalah perbandingan antara tegangan dan regangan. Modulus ini dapat disebut dengan sebutan Modulus Young.

   1. Tegangan (Stress)
      Tegangan adalah gaya per satuan luas penampang. Satuan tegangan adalah N/m² Secara matematis dapat dituliskan:
      
   2. Regangan (Strain)
      Regangan adalah perbandingan antara pertambahan panjang suatu batang terhadap panjang awal mulanya bila batang itu diberi gaya. Secara matematis dapat dituliskan:
      

   Dari kedua persamaan di atas dan pengertian modulus elastisitas, kita dapat mencari persamaan untuk menghitung besarnya modulus elastisitas, yang tidak lain adalah:
   

   Satuan untuk modulus elastisitas adalah N/m²
3. Gerak Benda di Bawah Pengaruh Gaya Pegas

   Bila suatu benda yang digantungkan pada pegas ditarik sejauh x meter dan kemudian dilepas, maka benda akan bergetar. Percepatan getarnya itu dapat dihitung dengan persamaan:
   

   Dari persamaan di atas, kita mengetahui bahwa besarnya percepatan getar (a) sebanding dan berlawanan arah dengan simpangan (x)

---

Hukum Kepler

Hukum Pertama

Figure 2: Hukum Kepler pertama menempatkan Matahari di satu titik fokus edaran elips.

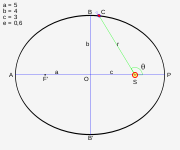
"Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya."

Pada zaman Kepler, klaim diatas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.

Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproximasi lingkaran. Jadi, kalau ditilik dari observasi jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh Pluto, yang diobservasi pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elipse dan kecil ukurannya.

Hukum Kedua

Figure 3: Illustrasi hukum Kepler kedua. Bahwa Planet bergerak lebih cepat didekat matahari dan lambat dijarak yang jauh. Sehingga jumlah area adalah sama pada jangka waktu tertentu.

"Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."

Secara matematis:

dimana 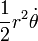adalah "areal velocity".

Hukum Ketiga

Planet yang terletak jauh dari matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepelr ketiga menjabarkan hal tersebut secara kuantitativ.

"Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari."

Secara matematis:

dimana P adalah period orbit planet dan a adalah axis semimajor orbitnya.

Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar matahari.

Elastisitas

adalah sifat suatu benda jika diberi gaya mengalami perubahan gaya, dan jika gaya di hilangkan kembali ke semula

Tegangan

Gaya per satuan Luas disebut juga sebagai tegangan. Secara matematis ditulis :

Satuan tegangan adalah N/m² (Newton per meter kuadrat)

Regangan

Regangan merupakan perbandingan antara perubahan panjang dengan panjang awal. Secara matematis ditulis :

Karena L sama-sama merupakan dimensi panjang, maka regangan tidak mempunyai satuan (regangan tidak mempunyai dimensi).

Regangan merupakan ukuran perubahan bentuk benda dan merupakan tanggapan yang diberikan oleh benda terhadap tegangan yang diberikan. Jika hubungan antara tegangan dan regangan dirumuskan secara matematis, maka akan diperoleh persamaan berikut :

Ini adalah persamaan matematis dari Modulus Elastis (E) alias modulus Young (Y). Jadi modulus elastis sebanding dengan Tegangan dan berbanding terbalik Regangan.

Hukum Hooke

s = E e

E = F/A : DL/L = F L/A DL

s = tegangan = beban persatuan luas = F/A
e = regangan = pertambahan panjang/panjang mula-mula = DL/L
E = modulus elastisitas = modulus Young
L = panjang mula-mula
c = konstanta gaya
DL = pertambahan panjang

Contoh:

1. Sebuah kawat baja (E = 2 x 10¹¹ N/m²). Panjang 125 cm dan diameternya 0.5 cm mengalami gaya tarik 1 N.Tentukan:

a. tegangan.
b. regangan.
c. pertambahan panjang kawat.

Jawab:

a. Tegangan = F/A ; F = 1 N.
A = p r² = 3.14 (1/4 . 10^-2)²
A = 1/(3.14 . 1/16 . 10^-4) = 16 . 10^-4/3.14 = 5.09 . 10⁴ N/M²

b. Regangan = e = DL/L = (F/A)/E
= 5.09. 10⁴/2.10¹¹ = 2.55.10^-7

c. Pertambahan panjang kawat: DL = e . L = 2.55 . 10^-7 . 125 = 3.2 . 10^-5 cm

Rangkaian pegas. Rangkaian seri 2 pegas atau lebih yang dirangkai secara seri akan memiliki nilai konstanta pegas total sebesar

Rangkaian paralel 2 pegas atau lebih yang dirangkai secara paralel akan memiliki nilai konstanta pegas total sebesar Ftot = F1 + F2 + .......Fn Gerak Harmonik Sederhana

Gerak Harmonik Sederhana (GHS) adalah gerak periodik dengan lintasan yang ditempuh selalu sama (tetap). Gerak Harmonik Sederhana mempunyai persamaan gerak dalam bentuk sinusoidal dan digunakan untuk menganalisis suatu gerak periodik tertentu. Gerak periodik adalah gerak berulang atau berosilasi melalui titik setimbang dalam interval waktu tetap. Gerak Harmonik Sederhana dapat dibedakan menjadi 2 bagian, yaitu :

• Gerak Harmonik Sederhana (GHS) Linier, misalnya penghisap dalam silinder gas, gerak osilasi air raksa / air dalam pipa U, gerak horizontal / vertikal dari pegas, dan sebagainya.
• Gerak Harmonik Sederhana (GHS) Angular, misalnya gerak bandul/ bandul fisis, osilasi ayunan torsi, dan sebagainya.

Beberapa Contoh Gerak Harmonik

• Gerak harmonik pada bandul: Sebuah bandul adalah massa (m) yang digantungkan pada salah satu ujung tali dengan panjang l dan membuat simpangan dengan sudut kecil. Gaya yang menyebabkan bandul ke posisi kesetimbangan dinamakan gaya pemulih yaitu dan panjang busur adalah Kesetimbangan gayanya. Bila amplitudo getaran tidak kecil namun tidak harmonik sederhana sehingga periode mengalami ketergantungan pada amplitudo dan dinyatakan dalam amplitudo sudut
• Gerak harmonik pada pegas: Sistem pegas adalah sebuah pegas dengan konstanta pegas (k) dan diberi massa pada ujungnya dan diberi simpangan sehingga membentuk gerak harmonik. Gaya yang berpengaruh pada sistem pegas adalah gaya Hooke,

Gerak Harmonis Sederhana pada Ayunan

Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.

Hubungan antara Periode dan Frekuensi

Frekuensi adalah banyaknya getaran yang terjadi selama satu detik/sekon. Dengan demikian selang waktu yang dibutuhkan untuk melakukan satu getaran adalah :

Selang waktu yang dibutuhkan untuk melakukan satu getaran adalah periode. Dengan demikian, secara matematis hubungan antara periode dan frekuensi adalah sebagai berikut :

Amplitudo (f)

Pada ayunan sederhana, selain periode dan frekuensi, terdapat juga amplitudo. Amplitudo adalah perpindahan maksimum dari titik kesetimbangan. Pada contoh ayunan sederhana sesuai dengan gambar di atas, amplitudo getaran adalah jarak AB atau BC.

Gerak Harmonis Sederhana pada Pegas

y = A Sin q = A Sin w t	Vy = dy/dt = wA cos wt	ay = dvy/dt =d2y/dt2 = -w2A sin wt ay = -w2y
A = ampiltudo getaran w = kecepatan anguler w = 2 pf = 2p/T ymaks = A (di titik tertinggi )	q = wt = 2pt/T = sudut fase vy maks = wA (dititik terendah/titik setimbang)	ay maks = w2 (pada saat membalik di titik tertinggi)

Energi Potensial pada Pegas Untuk menghitung energi potensial pada pegas, terlebih dahulu kita hitung kerja alias usaha yang dibutuhkan untuk meregangkan pegas. Persamaan Usaha adalah W = F s, di mana F adalah gaya dan s adalah perpindahan. Pada pegas, perpindahan adalah simpangan x. Ketika kita menekan atau meregangkan pegas sejauh x, dibutuhkan gaya Fa yang berbanding lurus dengan x. Secara matematis ditulis Fa = kx. Ketika ditekan atau diregangkan, pegas memberikan gaya dengan arah berlawanan (Fb) yang besarnya adalah Fb = -kx. Untuk menghitung energi potensial dari pegas yang tertekan atau teregang, terlebih dahulu kita hitung usaha atau kerja yang dibutuhkan untuk merentangkannya. Kita tidak bisa menggunakan persamaan usaha W = Fx, karena gaya Fa baik ketika pegas diregangkan maupun ditekan selalu berubah-ubah sepanjang x. (amati gambar di atas). Oleh karena itu kita menggunakan gaya rata-rata. Gaya Fa berubah dari 0 ketika x=0 sampai bernilai kx ketika pegas diregangkan atau ditekan sejauh x. Gaya rata-rata = F = ½ (0 + kx) = ½ kx. x adalah jarak maksimum pegas yang diregangkan atau ditekan. Usaha alias kerja yang dilakukan adalah : W = Fa x = (1/2 kx) (x) = ½ kx2 Dengan demikian, nilai Energi Potensial elastis adalah : EP elastis = ½ kx2 Energi Kinetik pada Pegas Perlu anda ketahui bahwa Energi Potensial tidak mempunyai suatu persamaan umum yang mewakili semua jenis gerakan. Untuk EP elastis telah kita turunkan pada pembahasan di atas. Berbeda dengan EP, persamaan EK bersifat umum untuk semua jenis gerakan. Energi Kinetik dimiliki benda ketika bergerak. Besar energi kinetik adalah : EK = ½ mv2 m adalah massa benda dan v adalah kecepatan gerak benda. Jumlah total Energi Kinetik dan Energi Potensial dari pegas adalah Energi Mekanik. Energi tersebut bernilai tetap alias kekal. Secara matematis ditulis : EM = EP + EK Energi Potensial sebuah pegas dengan konstanta gaya k yang teregang sejauh x dari kesetimbangannya dinyatakan dengan persamaan : EP = ½ kx2 Energi Kinetik sebuah benda bermassa m yang bergerak dengan kelajuan v ialah : EK = ½ mv2 Energi Total (Energi Mekanik) adalah jumlah Energi Potensial dan Energi Kinetik : EM = EP + EK = ½ kx2 + ½ mv2 Ketika benda berada pada simpangan maksimum, x = A (A = Amplitudo), kecepatan benda = 0, sehingga Energi Mekanik benda : EM = ½ kA2 Persamaan ini memberikan sifat umum penting yang dimiliki Gerak Harmonik Sederhana (GHS) : Energi total pada Gerak Harmonik Sederhana berbanding lurus dengan kuadrat amplitudo.

Materi Fisika Semester 2

Usaha

dilambangkan dengan huruf W digambarkan sebagai sesuatu yang dihasilkan oleh Gaya (F) ketika Gaya bekerja pada benda hingga benda bergerak dalam jarak tertentu. Hal yang paling sederhana adalah apabila Gaya (F) bernilai konstan (baik besar maupun arahnya) dan benda yang dikenai Gaya bergerak pada lintasan lurus dan searah dengan arah Gaya tersebut.

Secara matematis, usaha yang dilakukan oleh gaya yang konstan didefinisikan sebagai hasil kali perpindahan dengan gaya yang searah dengan perpindahan.

Persamaan matematisnya adalah :

W = Fs cos 0 = Fs (1) = Fs

W adalah usaha alias kerja, F adalah besar gaya yang searah dengan perpindahan dan s adalah besar perpindahan.

Apabila gaya konstan tidak searah dengan perpindahan, sebagaimana tampak pada gambar di bawah, maka usaha yang dilakukan oleh gaya pada benda didefinisikan sebagai perkalian antara perpindahan dengan komponen gaya yang searah dengan perpindahan. Komponen gaya yang searah dengan perpindahan adalah F cos teta

Secara matematis dirumuskan sebagai berikut :

Hasil perkalian antara besar gaya (F) dan besar perpindahan (s) di atas merupakan bentuk perkalian titik atau perkalian skalar. Karenanya usaha masuk dalam kategori besaran skalar. Pelajari lagi perkalian vektor dan skalar kalau dirimu bingun… Persamaan di atas bisa ditulis dalam bentuk seperti ini :

Satuan Usaha dalam Sistem Internasional (SI) adalah newton-meter. Satuan newton-meter juga biasa disebut Joule ( 1 Joule = 1 N.m). menggunakan sistem CGS (Centimeter Gram Sekon), satuan usaha disebut erg. 1 erg = 1 dyne.cm. Dalam sistem British, usaha diukur dalam foot-pound (kaki-pon). 1 Joule = 10⁷ erg = 0,7376 ft.lb.

Perlu anda pahami dengan baik bahwa sebuah gaya melakukan usaha apabila benda yang dikenai gaya mengalami perpindahan. Jika benda tidak berpindah tempat maka gaya tidak melakukan usaha. Agar memudahkan pemahaman anda, bayangkanlah anda sedang menenteng buku sambil diam di tempat. Walaupun anda memberikan gaya pada buku tersebut, sebenarnya anda tidak melakukan usaha karena buku tidak melakukan perpindahan. Ketika anda menenteng atau menjinjing buku sambil berjalan lurus ke depan, ke belakang atau ke samping, anda juga tidak melakukan usaha pada buku. Pada saat menenteng buku atau menjinjing tas, arah gaya yang diberikan ke atas, tegak lurus dengan arah perpindahan. Karena tegak lurus maka sudut yang dibentuk adalah 90^o. Cos 90^o = 0, karenanya berdasarkan persamaan di atas, nilai usaha sama dengan nol. Contoh lain adalah ketika dirimu mendorong tembok sampai puyeng… jika tembok tidak berpindah tempat maka walaupun anda mendorong sampai banjir keringat, anda tidak melakukan usaha. Kita dapat menyimpulkan bahwa sebuah gaya tidak melakukan usaha apabila gaya tidak menghasilkan perpindahan dan arah gaya tegak lurus dengan arah perpindahan.

ENERGI

Energi merupakan salah satu konsep yang paling penting dalam fisika. Konsep yang sangat erat kaitannya dengan usaha adalah konsep energi. Secara sederhana, energi merupakan kemampuan melakukan usaha. Definisi yang sederhana ini sebenarnya kurang tepat atau kurang valid untuk beberapa jenis energi (misalnya energi panas atau energi cahaya tidak dapat melakukan kerja). Definisi tersebut hanya bersifat umum. Secara umum, tanpa energi kita tidak dapat melakukan kerja. Sebagai contoh, jika kita mendorong sepeda motor yang mogok, usaha alias kerja yang kita lakukan menggerakan sepeda motor tersebut.

Misalnya ketika kita menyalakan lampu neon, energi listrik berubah menjadi energi cahaya. Energi listrik juga bisa berubah menjadi energi panas (setrika listrik), energi gerak (kipas angin) dan sebagainya. Banyak sekali contoh dalam kehidupan kita, dirimu bisa memikirkan contoh lainnya. Secara umum, energi bermanfaat bagi kita ketika energi mengalami perubahan bentuk, misalnya energi listrik berubah menjadi energi gerak (kipas angin), atau energi kimia berubah menjadi energi gerak (mesin kendaraan).

ENERGI MEKANIK (EM)

EM = Ek + Ep

Nilai EM selalu tetap/sama pada setiap titik di dalam lintasan suatu benda.


Pemecahan soal fisika, khususnya dalam mekanika, pada umumnya didasarkan pada HUKUM KEKEKALAN ENERGI, yaitu energi selalu tetap tetapi bentuknya bisa berubah; artinya jika ada bentuk energi yang hilang harus ada energi bentuk lain yang timbul, yang besarnya sama dengan energi yang hilang tersebut.
Ek + Ep = EM = tetap

Ek1 + Ep1 = Ek2 + Ep2




PRINSIP USAHA-ENERGI

Jika pada peninjauan suatu soal, terjadi perubahan kecepatan akibat gaya yang bekerja pada benda sepanjang jarak yang ditempuhnya, maka prinsip usaha-energi berperan penting dalam penyelesaian soal tersebut

W tot = DEk ® S F.S = Ek akhir - Ek awal

W tot = jumlah aljabar dari usaha oleh masing-masing gaya
= W1 + W2 + W3 + .......

D Ek = perubahan energi kinetik = Ek akhir - Ek awal



ENERGI POTENSIAL PEGAS (Ep)
Ep = 1/2 k D x2 = 1/2 Fp Dx

Fp = - k Dx


Dx = regangan pegas
k = konstanta pegas
Fp = gaya pegas

Tanda minus (-) menyatakan bahwa arah gaya Fp berlawanan arah dengan arah regangan x.

2 buah pegas dengan konstanta K1 dan K2 disusun secara seri dan paralel: seri paralel
1 = 1 + 1
Ktot K1 K2 Ktot = K1 + K2

Momentum,Impuls,Tumbukan

A. Pengertian Momentum.
Momentum suatu benda adalah hasil kali massa dan kecepatan.
Dirumuskan dengan persamaan:

p = m.v m = massa ( kg)
v = kecepatan ( m/s )
p = momentum ( kg.m/s )
Momentum juga disebut jumlah gerak.
Momentum adalah besaran vector. Momentum 45 kgm/s ke utara berbeda dengan momentum 45 kgm/s ke selatan, walaupun nilai keduanya sama. Penjumlahan momentum mengikuti aturan penjumlahan vector. Misal momentum p1 dan p2 membentuk sudut α , maka resultan/ jumlah kedua momentum tersebut dapayt dituliskan dengan persamaan :
p1
p
p2
α –––––––––––––––––––––––––––––––
p = √ p12 + p22 + 2 p1 p2 cos α

B. Pengetian Impuls.
Impuls adalah hasil kali antara gaya yang bekerja dan selang waktu gaya itu bekerja. Impuls juga sering disebut pukulan.
Dirumuskan dengan persamaan :

I = F. ∆t F = gaya ( N )
∆t = selang waktu ( s )
I = Impuls ( Ns )
Impuls merupakan besaran vector.
C. Hubungan antara imupls dan momentum.
Sebuah benda massa m mula-mula bergerak dengan kecepatan v1, kemudian dipukul dengan gaya F hingga kecepatannya menjadi v2, seperti gambar di bawah, maka besarnya impuls yang bekerja pada benda tersebut adalah:
∆t
v1
v2
F

m m

Sesuai dengan hukum II Newton:

I = F. ∆t , karena
v2 – v1
F = m.a dan a = –––––––––––, maka :
∆t
v2 – v1
I = m.–––––– . ∆t
∆t
I = m (v2 – v1 ) –––––> I = m v2 – m v1 atau I = p2 – p1

Dapat juga dituls I = ∆p ( Impuls merupakan perubahan momentum benda )
Contoh Soal
Sebuah benda massa 5 kg bergerak dengan kecepatan 10m/s. Hitunglah momentum yang dimiliki benda!
Penyelesian : Diketahui : m = 5 kg; v = 10 m/s
Ditanya : p = …?
Jaab : p = m.v = 5.10 = 50 kgm/s

Sebuah benda mula-mula bergerak ke utara dengan kecepatan 6 m/s, kemudian berbelok ke barat dengan kecepatan 8 m/s. Apabila massa benda 50 kg, berpakah momentum total yang dimiliki benda ?
Penyelesaian : Diketahui : v1 = 6 m/s; v2 = 8 m/s; m = 5 kg
Ditanya : p = …?
Jawab : p1 = m. v1 = 50.6 = 300 kgm/s
p1
p
P2 P2 = m. v2 = 50.8 = 400 kgm/s

––––––– –––––––––
p = √ p12 + p22 = √ 3002 + 4002 = 500 kgm/s

Sebuah gaya 25 N bekerja pada sebuah benda dalam selang waktu 0,2 sekon. Hitunglah impuls yang dikerjakan gaya tersebut pada benda
Penyelesaian : Diketahui : F = 25 N; ∆t = 0,2 s
Ditanya : I = …?
Jawab : I = F. ∆t = 25. 0,2 = 5 Ns

Sebuah bola massanya 50 gram dilempar dengan kecepatan 10 m/s, kemudian dipukul dengan gaya F hingga kecepatannya 20 m/s berlawanan arah dengan kecepatan semula.
Hitunglah impuls yang dikerjakan oleh gaya tersebut!
Jika besarnya gaya F = 150 N, berapa lama pemukul menyentuh bola?
Penyelesaian : Diketahui : m = 50 gram = 50.10–3 kg; v1 = – 10 m/s;
v2 = 20 m/s
Ditanya : a. I = …?
b. Jika F = 150 N –––> ∆t = …?
Jawab : a. I = m.( v2 – v1 ) = 50.10–3 [20 – (-10)]
= 50.10–3. 30 = 1500.10–3 = 1,5 Ns
b. I = F. ∆t ––––> 1,5 = 150. ∆t –––> ∆t = 0,01 s
D. Hukum Kekekalan Momentum dan Tumbukan.
“Jumlah momentum suatu sistem sebelum dan sesudah tumbukan akan selalu tetap”
Pernyataan di atas disebut hukum kekekalan momentum dan ditulis dengan persamaan:

m1.v1 + m2.v2 = m1.v1’ + m2.v2’ m1 = massa benda 1
m2 = massa benda 2
v1 = kecepatan benda 1 sebelum tumbukan
v2 = kecepatan benda 2 sebelum tumbukan
v1’ = kecepatan benda 1 sesudah tumbukan
v2’ = kecepatan benda 2 sesudah tumbukan

Jenis-jenis Tumbukan
a. Tumbukan lenting sempurna (elastis sempurna)
Tumbukan lenting sempurna yaitu tumbukan dimana tidak ada energi kinetik yang hilang dari sistem. Dalam tumbukan ini berlaku hukum kekekalan momentum dan hukum kekekalan energi kinetik.
Dalam hal ini berlaku persamaan :
m1.v1 + m2.v2 = m1.v1’ + m2.v2’ ……………………….(1) dan
½ m1.v12 + ½ m2.v22 = ½ m1.(v1’)2 + ½ m2.(v2’)2 ……..(2)

Dengan membagi persamaan (2) dengan persamaan (1), maka akan didapatkan

persamaan : v1 + v1’ = v2 + v2’

b. Tumbukan tidak lenting sama sekali
Pada tumbukan tidak lenting sama sekali, sesudah tumbukan kedua benda bergabung menjadi satu dan bergerak bersama-sama. Dengan demikian, maka kecepatan kedua benda setelah bertumbukan adalah sama.: v1’ = v2’ = v’
Pada tumbukan ini persamaan hukum kekekalan momentum dapat ditulis sbb:

m1.v1 + m2.v2 = m1.v1’ + m2.v2’, karena v1’ = v2’ = v’, maka
m1.v1 + m2.v2 = m1.v’ + m2.v’
atau dapat juga ditulis :
m1.v1 + m2.v2 = (m1 + m2).v’

v’ = kecepatan benda setelah tumbukan ( m/s )

Momentum Anguler

Benda-benda yang berotasi cenderung mempertahankan keadaan awalnya (tetap berputar). Sebuah gasing akan terus berputar jika tidak ada friksi yang memperlambatnya.

Jika pada gerak lurus kita mengenal momentum linier, yaitu p = m v , maka analog dengan besaran tersebut, ada besaran momentum anguler (L) yang didefinisikan sebagai :

Momentum anguler : = m x

Dengan r = vector posisi relative terhadap titik poros

harga L dapat dituliskan sebagai : L= m (r) (ω r) sin θ

L= m r² sin θ ω

atau

L= I ω

Bila resultan momen gaya yang bekerja pada suatu system partikel adalah nol, momentum anguler total system tersebut tetap harganya (konstan);

L₁ = L₂

atau

I₁ ω₁ = I₂ ω₂ persamaan ini menyatakan kekekalan momentum anguler.

Keseimbangan

1. Keseimbangan Pertikel

Sebuah partikel atau benda titik dikatakan seimbang jika resultan gaya-gaya yang bekerja padanya sama dengan nol.

Σ F = 0

Partikel atau benda titik yang seimbang, mungkin berada dalam salah satu dari dua keadaan berikut :

Diam, disebut seimbang statis

Bergerak dengan kecepatan konstan, disebut seimbang dinamis

2. Momen Gaya (Torsi)

Momen gaya atau torsi pada sebuah benda menyebabkan benda tersebut berotasi. Ia didefinisikan sebagai berikut (momen dari gaya F terhadap poros, sumbu putar, O)

τ = F Lт atau τ = Fт L

catatan.

Momen gaya yang menyebabkan rotasi searah jarum jam diberi tanda positif.

Momen gaya yang menyebabkan rotasi berlawanan arah jarum jam diberi tanda negative.

3. Momen Kopel

Kopel adalah dua buah gaya yang sama besar, berlawanan arah, tetapi tidak segaris kerja. Kopel yang bekerja pada sebuah benda menghasilkan rotasi murni.

Momen kopel dapat dinyatakan sebagai berikut :

M = F d

4. Resultan Gaya Sejajar

Gaya-gaya sejajar mempunyai resultan gaya letak titik tangkapnya sedemikian rupa sehingga resultan momen gaya terhadap titik tersebut adalah nol.

Resultan gaya : F_R = F₁ + F₂

5. Keseimbangan Benda Tegar

Benda yang tidak berubah bentuk ketika dipengaruhi oleh gaya dinamakan benda tegar. Benda tegar dapat bergerak translasi murni, rotasi murni, atau kombinasi keduanya. Bneda tegar dikatakan seimbang bila memenuhi syarat keseimbangan translasi dan keseimbangan rotasi, yaitu :

ΣF = 0 dan Στ = 0

6. Titik Pusat Massa dan Titik (Pusat) Berat

6.1. Titik Pusat Massa

Titik pusat massa adalah sebuah titik dimana seluruh benda dapat dipusatkan padanya. Jika resultan gaya bekerja melelui titik pusat massa, maka benda akan bergerak translasi murni.

Untuk system benda dua dimensi, letak titik pusat massa dinyatakan dengan koordinat (x_pm , y_pm), dengan :

X_pm = dan y_pm =

6.2. Titik Pusat Berat

Titik pusat berat adalah titik tangkap gaya berat yang bekerja pada sebuah benda.

Untuk system benda dua dimensi, letak titik pusat berat dinyatakan dengan koordinat (x_pb , y_pb), dengan :

X_pb = dan y_pb =

Letak titk pusat massa benda pada umumnya tidak sama dengan letak titik pusat berat benda.

Untuk benda yang letaknya dekat dengan permukaan bumi, dimana g dianggap konstan, letak pusat massa dan titik berat sebuah benda dapat dianggap berhimpit.

Koordinat pusat massa Sistem Partikel (benda tak kontinu) :

X_pm = =

dan

y_pm = =

Absis pusat massa benda homogeny 1 dimensi :

X_pm = l = panjang

Absis pusat massa benda homogeny 2 dimensi :

X_pm = A = luas

Absis pusat massa benda homogeny 3 dimensi :

X_pm = V = volume

7. Jenis Keseimbangan

Keadaan keseimbangan suatu benda dapat digolongkan ke dalam salah satu dari 3 jenis keseimbangan berikut :

Kesimbangan Stabil

Benda di katakana dalam keseimbangan stabil bila benda diberi sedikit usikan, dan kemudian usikan dihilangkan, benda kembali ke posisi keseimbangan semula.

GAS IDEAL

Hukum Boyle

Berdasarkan percobaan yang dilakukannya, om Robert Boyle menemukan bahwa apabila suhu gas dijaga agar selalu konstan, maka ketika tekanan gas bertambah, volume gas semakin berkurang. Demikian juga sebaliknya ketika tekanan gas berkurang, volume gas semakin bertambah. Istilah kerennya tekanan gas berbanding terbalik dengan volume gas. Hubungan ini dikenal dengan julukan Hukum Boyle. Secara matematis ditulis sebagai berikut :

Keterangan :

Hukum Gay-Lussac

Setelah om obet Boyle dan om Charles mengabadikan namanya dalam ilmu fisika, om Joseph Gay-Lussac pun tak mau ketinggalan. Berdasarkan percobaan yang dilakukannya, om Jose menemukan bahwa apabila volume gas dijaga agar selalu konstan, maka ketika tekanan gas bertambah, suhu mutlak gas pun ikut2an bertambah. Demikian juga sebaliknya ketika tekanan gas berkurang, suhu mutlak gas pun ikut2an berkurang. Istilah kerennya, pada volume konstan, tekanan gas berbanding lurus dengan suhu mutlak gas. Hubungan ini dikenal dengan julukan Hukum Gay-Lussac. Secara matematis ditulis sebagai berikut :

Hubungan antara suhu, volume dan tekanan gas

Hukum Boyle, hukum Charles dan hukum Gay-Lussac baru menurunkan hubungan antara suhu, volume dan tekanan gas secara terpisah. Bagaimanapun ketiga besaran ini memiliki keterkaitan erat dan saling mempengaruhi. Karenanya, dengan berpedoman pada ketiga hukum gas di atas, kita bisa menurunkan hubungan yang lebih umum antara suhu, volume dan tekanan gas. Gurumuda tulis lagi ketiga perbandingan di atasbiar dirimu lebih nyambung :

Jika perbandingan 1, perbandingan 2 dan perbandingan 3 digabung menjadi satu, maka akan tampak seperti ini :

Persamaan ini menyatakan bahwa tekanan (P) dan volume (V) sebanding dengan suhu mutlak (T). Sebaliknya, volume (V) berbanding terbalik dengan tekanan (P).

Perbandingan 4 bisa dioprek menjadi persamaan :

Keterangan :

P₁ = tekanan awal (Pa atau N/m²)

P₂ = tekanan akhir (Pa atau N/m²)

V₁ = volume awal (m³)

V₂ = volume akhir (m³)

T₁ = suhu awal (K)

T₂ = suhu akhir (K)

(Pa = pascal, N = Newton, m² = meter kuadrat, m³ = meter kubik, K = KelvIN)

HUKUM GAS IDEAL (dalam jumlah mol)

Setelah terseok-seok, akhirnya kita tiba di penghujung acara pengoprekan rumus. Perbandingan 6 (tuh di atas) bisa kita tulis menjadi persamaan, dengan memasukan jumlah mol (n) dan konstanta gasuniversal (R)…

PV = nRT

Persamaan ini dikenal dengan julukan hukum gas ideal alias persamaan keadaan gas ideal.

Keterangan :

P = tekanan gas (N/m²)

V = volume gas (m³)

n = jumlah mol (mol)

R = konstanta gas universal (R = 8,315 J/mol.K)

T = suhu mutlak gas (K)

Contoh soal :

Tentukan volume 2 mol gas pada STP (anggap saja gas ini adalah gas ideal)

Panduan jawaban :

Volume 2 mol gas pada STP (temperatur dan tekanan stadard) adalah 44,8 liter.

HUKUM GAS IDEAL (Dalam jumlah molekul)

Kalau sebelumnya Hukum gas ideal dinyatakan dalam jumlah mol (n), maka kali ini hukum gas ideal dinyatakan dalam jumlah molekul (N). Sebelum menurunkan persamaannya, terlebih dahulu baca pesan-pesan berikut ini…

Seperti yang telah gurumuda jelaskan sebelumnya, apabila kita menyatakan ukuran zat tidak dalam bentuk massa (m), tapi dalam jumlah mol (n), maka konstanta gas universal (R) berlaku untuk semua gas. Hal ini pertama kali ditemukan oleh alhamrum Amedeo Avogadro (1776-1856), mantan ilmuwan Italia. Sekarang beliau sudah beristirahat di alam baka… Almahrum Avogadro mengatakan bahwa ketika volume, tekanan dan suhu setiap gas sama, maka setiap gas tersebut memiliki jumlah molekul yang sama. Kalimat yang dicetak tebal ini dikenal dengan julukan hipotesa Avogadro (hipotesa = ramalan atau dugaan). Hipotesa almahrum Avogadro ini sesuai dengan kenyataan bahwa konstanta R sama untuk semua gas. Berikut ini beberapa pembuktiannya :

Pertama, jika kita menyelesaikan soal menggunakan persamaan hukum gas ideal (PV = nRT), kita akan menemukan bahwa ketika jumlah mol (n) sama, tekanan dan suhu juga sama, maka volume semua gas akan bernilai sama, apabila kita menggunakan konstanta gas universal (R = 8,315 J/mol.K). Karenanya dirimu jangan pake heran kalau pada STP, setiap gas yang memiliki jumlah mol (n) yang sama akan memiliki volume yang sama. Volume 1 mol gas pada STP = 22,4 liter. Volume 2 mol gas = 44,8 liter. Volume 3 mol gas = 67,2 liter. Dan seterusnya… ini berlaku untuk semua gas.

Kedua, jumlah molekul dalam 1 mol sama untuk semua gas. Jumlah molekul dalam 1 mol = jumlah molekul per mol = bilangan avogadro (N_A). Jadi bilangan Avogadro bernilai sama untuk semua gas. Besarnya bilangan Avogadro diperoleh melalui pengukuran :

N_A = 6,02 x 10²³ molekul/mol = 6,02 x 10²³ /mol

= 6,02 x 10²⁶ molekul/kmol = 6,02 x 10²⁶ /kmol

Untuk memperoleh jumlah total molekul (N), maka kita bisa mengalikan jumlah molekul per mol (N_A) dengan jumlah mol (n).

Kita oprek lagi persamaan Hukum Gas Ideal :

Ini adalah persamaan Hukum Gas Ideal dalam bentuk jumlah molekul.

Keterangan :

P = Tekanan

V = Volume

N = Jumlah total molekul

k = Konstanta Boltzmann (k = 1,38 x 10^-13 J/K)

T = Suhu

TERMODINAMIKA

Termodinamika adalah kajian tentang kalor (panas) yang berpindah. Dalam termodinamika kamu akan banyak membahas tentang sistem dan lingkungan. Kumpulan benda-benda yang sedang ditinjau disebut sistem, sedangkan semua yang berada di sekeliling (di luar) sistem disebut lingkungan. Usaha Luar Usaha luar dilakukan oleh sistem, jika kalor ditambahkan (dipanaskan) atau kalor dikurangi (didinginkan) terhadap sistem. Jika kalor diterapkan kepada gas yang menyebabkan perubahan volume gas, usaha luar akan dilakukan oleh gas tersebut. Usaha yang dilakukan oleh gas ketika volume berubah dari volume awal V1 menjadi volume akhir V2 pada tekanan p konstan dinyatakan sebagai hasil kali tekanan dengan perubahan volumenya. W = p∆V= p(V2 – V1) Secara umum, usaha dapat dinyatakan sebagai integral tekanan terhadap perubahan volume yang ditulis sebagai pers01Tekanan dan volume dapat diplot dalam grafik p – V. jika perubahan tekanan dan volume gas dinyatakan dalam bentuk grafik p – V, usaha yang dilakukan gas merupakan luas daerah di bawah grafik p – V. hal ini sesuai dengan operasi integral yang ekuivalen dengan luas daerah di bawah grafik. fig2004Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < >Energi Dalam Suatu gas yang berada dalam suhu tertentu dikatakan memiliki energi dalam. Energi dalam gas berkaitan dengan suhu gas tersebut dan merupakan sifat mikroskopik gas tersebut. Meskipun gas tidak melakukan atau menerima usaha, gas tersebut dapat memiliki energi yang tidak tampak tetapi terkandung dalam gas tersebut yang hanya dapat ditinjau secara mikroskopik. Berdasarkan teori kinetik gas, gas terdiri atas partikel-partikel yang berada dalam keadaan gerak yang acak. Gerakan partikel ini disebabkan energi kinetik rata-rata dari seluruh partikel yang bergerak. Energi kinetik ini berkaitan dengan suhu mutlak gas. Jadi, energi dalam dapat ditinjau sebagai jumlah keseluruhan energi kinetik dan potensial yang terkandung dan dimiliki oleh partikel-partikel di dalam gas tersebut dalam skala mikroskopik. Dan, energi dalam gas sebanding dengan suhu mutlak gas. Oleh karena itu, perubahan suhu gas akan menyebabkan perubahan energi dalam gas. Secara matematis, perubahan energi dalam gas dinyatakan sebagai untuk gas monoatomik Hukum I Termodinamika Jika kalor diberikan kepada sistem, volume dan suhu sistem akan bertambah (sistem akan terlihat mengembang dan bertambah panas). Sebaliknya, jika kalor diambil dari sistem, volume dan suhu sistem akan berkurang (sistem tampak mengerut dan terasa lebih dingin). Prinsip ini merupakan hukum alam yang penting dan salah satu bentuk dari hukum kekekalan energi. Sistem yang mengalami perubahan volume akan melakukan usaha dan sistem yang mengalami perubahan suhu akan mengalami perubahan energi dalam. Jadi, kalor yang diberikan kepada sistem akan menyebabkan sistem melakukan usaha dan mengalami perubahan energi dalam. Prinsip ini dikenal sebagai hukum kekekalan energi dalam termodinamika atau disebut hukum I termodinamika. Secara matematis, hukum I termodinamika dituliskan sebagai Q = W + ∆U Dimana Q adalah kalor, W adalah usaha, dan ∆U adalah perubahan energi dalam. Secara sederhana, hukum I termodinamika dapat dinyatakan sebagai berikut. Jika suatu benda (misalnya krupuk) dipanaskan (atau digoreng) yang berarti diberi kalor Q, benda (krupuk) akan mengembang atau bertambah volumenya yang berarti melakukan usaha W dan benda (krupuk) akan bertambah panas (coba aja dipegang, pasti panas deh!) yang berarti mengalami perubahan energi dalam ∆U. Proses Isotermik Suatu sistem dapat mengalami proses termodinamika dimana terjadi perubahan-perubahan di dalam sistem tersebut. Jika proses yang terjadi berlangsung dalam suhu konstan, proses ini dinamakan proses isotermik. Karena berlangsung dalam suhu konstan, tidak terjadi perubahan energi dalam (∆U = 0) dan berdasarkan hukum I termodinamika kalor yang diberikan sama dengan usaha yang dilakukan sistem (Q = W). Proses Isokhorik Jika gas melakukan proses termodinamika dalam volume yang konstan, gas dikatakan melakukan proses isokhorik. Karena gas berada dalam volume konstan (∆V = 0), gas tidak melakukan usaha (W = 0) dan kalor yang diberikan sama dengan perubahan energi dalamnya. Kalor di sini dapat dinyatakan sebagai kalor gas pada volume konstan QV. QV = ∆U Proses Isobarik Jika gas melakukan proses termodinamika dengan menjaga tekanan tetap konstan, gas dikatakan melakukan proses isobarik. Karena gas berada dalam tekanan konstan, gas melakukan usaha (W = p∆V). Kalor di sini dapat dinyatakan sebagai kalor gas pada tekanan konstan Qp. Berdasarkan hukum I termodinamika, pada proses isobarik berlaku pers05Sebelumnya telah dituliskan bahwa perubahan energi dalam sama dengan kalor yang diserap gas pada volume konstan QV =∆U Dari sini usaha gas dapat dinyatakan sebagai W = Qp − QV Jadi, usaha yang dilakukan oleh gas (W) dapat dinyatakan sebagai selisih energi (kalor) yang diserap gas pada tekanan konstan (Qp) dengan energi (kalor) yang diserap gas pada volume konstan (QV). Proses Adiabatik Dalam proses adiabatik tidak ada kalor yang masuk (diserap) ataupun keluar (dilepaskan) oleh sistem (Q = 0). Dengan demikian, usaha yang dilakukan gas sama dengan perubahan energi dalamnya (W = ∆U). Jika suatu sistem berisi gas yang mula-mula mempunyai tekanan dan volume masing-masing p1 dan V1 mengalami proses adiabatik sehingga tekanan dan volume gas berubah menjadi p2 dan V2, usaha yang dilakukan gas dapat dinyatakan sebagai pers06Dimana γ adalah konstanta yang diperoleh perbandingan kapasitas kalor molar gas pada tekanan dan volume konstan dan mempunyai nilai yang lebih besar dari 1 (γ > 1). Proses adiabatik dapat digambarkan dalam grafik p – V dengan bentuk kurva yang mirip dengan grafik p – V pada proses isotermik namun dengan kelengkungan yang lebih curam.

MATERI FISIKA KELAS XII SEMESTER 1

A.Gerak Harmonik Sederhana

Gerak harmonik merupakan gerak suatu partikel atau benda, dengan gerak posisi partikel sebagai fungsi waktu berupa sinusoidal(dapat dinyatakan dalam bentuk sinus atau cosines). Contoh gerak harmonic diantaranya gerak pada pegas,gerak pada bandul atau ayunaan sederhana dan gerak melingkar. Gerak harmonic merupakan gerak periodic, yaitu gerak bolak – balik secara periodic melalui titik keseimbangan. Pegas yang diberi simpangan sejauh y dari posisi keseimbangannya akan bergerak bolak – balik melalui titik keseimbNgn tersebut ketika dilepaskan. Gerakan ini disebabkan oleh gaya pemulih yang bekerja pada pegas. Gaya pemulih ini berusaha untuk mengembalikan posisi benda ke posisi keseimbangannya. Besar gaya pemulih berbanding lurus dengan besar simpangan dan arahnya berlaanan dengan arah simpangan. Secara matematis besar gaya pemulih pada pegas dapat ditulis sebagai berikut:

F = - k y Keterangan: K = tetapan pegas (N/m) y = simpangan (m) F = gaya pemulih (N) (tanda minus menyatakan bahwa arah gaya pemulih berlawanan dengan arah simpangan) Besaran lain yang juga penting dalam gerak harmonic adalah periode dan frekwensi.

Periode dari suatu pegas yang bergetar dinyatakan melalui hubungan berikut:

T = 2π√(m/k)

Keterangan :
M = masa benda (kg)
π = 3,14
k = tetapan pegas (N/m)
T = periode (s)

Frekuensi merupakan kebalikan dari periode sehingga kita dapat menurunkan persamaan periodenya.

Gambar Getaran yang dihasilkan oleh bandul

Gambar diatas menunjukkan sebuah benda bermassa m di gantungkan pada seutas tali yang panjangnya l. kemudian benda tersebut diberi simpangan sehingga benda bergerak bolak – balik juga merupakan gaya pemulih. Namun besar gaya pemulihnya dapat dinyatakan melalui hubungan berikut:

F= -ω sin⁡θ

Dengan :
ω = berat bandul (N)
θ = sudut simpangan bandul terhadap sumbu vertical
F = gaya pemulih (N)
Dalam hal ini, tanda minus (-) juga menunukkan arah gaya pemulih yang berlawanan dengan arah simpangan.

Periode dari gerakan bandul dinyatakan melalui hubungan berikut :

T= 2π√(l/g)

Dengan :
l = panjang bandul (m)
g = percepatan gravitasi (m/s2)
π = 3,14
T = periode ayunan (s)

Kebalikan dari periode adalah frekuensi. Kamu dapat mencarinya dengan cara yang sama seperti diatas.
Contoh lain dari gerak harmonic sederhana adalah gerak melingkar. Simpangan gerak harmonic sederhana dapat dianggap sebagai proyeksi gerak melingkar pada suatu lingkaran.
Gambar dibawah ini menunjukkan sebuah partikel yang bergerak sepanjang lintasan lingkaran yang berjari – jari A dengan kecepatan sudut w. missalkan mula – mula partikel berada di P1. Setelah beberapa saat (t), partikel tersebut berada di P2. Maka jauhnya lintasan yang ditempuh oleh partikel tersebut dari titik P1 ke P2 adalah :

Posisi simpangan P pada suatu saat tertentu dalam gerak melingkar

y = A sin θ atau y = A sin 2π/T t

Jika benda mula – mula berada pada posisi θ0 maka perumusan simpangan diatas dapat dituliskan sebagai berikut:

y = A sin (θ + θ0 atau y = A sin ( 2π/T t + θ0)

atau

y = A sin (2πft + θ0)

'

Contoh soal:
Sebuah partikel melakukan gerak harmonic sederhana dengan frekuensi 0,2 Hz. Jika simpangan maksimum yang dapat dicapai oleh partikel tersebut adalah 10 cm, tentukanlah simpangan partikel tersebut pada saat t = 2 sekon!!!

Penyelesaian

Diketahui:
f = 0,2 Hz
A = 10 cm = 0,1 m
t = 2 sekon
y = A sin 2πf.t = 0,1 . sin 2π (0,2).2
= 0,1. Sin 0,8 π = 0,1 . 0,59
= 0,059 m = 5,9 cm

Dalam hal ini, kita mengenal besaran fase getaran yang didefinisikan sebagai perbandingan antara waktu sesaat benda (t) dan waktu yang diperlukan untuk bergerak satu putaran penuh (T).

φ = t/T

θ=wt

θ=2π/T t

t/T=θ/2π=φ

Dengan : θ = sudut fase φ =fase getaran

1. Jenis, Contoh, dan Besaran Fisika pada Gerak Harmonik Sederhana

1. 1. Jenis Gerak Harmonik Sederhana

Gerak Harmonik Sederhana dapat dibedakan menjadi 2 bagian, yaitu^[1] :

• Gerak Harmonik Sederhana (GHS) Linier, misalnya penghisap dalam silinder gas, gerak osilasi air raksa / air dalam pipa U, gerak horizontal / vertikal dari pegas, dan sebagainya.
• Gerak Harmonik Sederhana (GHS) Angular, misalnya gerak bandul/ bandul fisis, osilasi ayunan torsi, dan sebagainya.

Contoh gerak harmonik sederhana

1. 2. Beberapa Contoh Gerak Harmonik Sederhana

• Gerak harmonik pada bandul

Gerak harmonik pada bandul

Ketika beban digantungkan pada ayunan dan tidak diberikan gaya, maka benda akan dian di titik keseimbangan B^[2]. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A^[2]. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana^[2].

• Gerak harmonik pada pegas

Gerak vertikal pada pegas

Semua pegas memiliki panjang alami sebagaimana tampak pada gambar^[2]. Ketika sebuah benda dihubungkan ke ujung sebuah pegas, maka pegas akan meregang (bertambah panjang) sejauh y. Pegas akan mencapai titik kesetimbangan jika tidak diberikan gaya luar (ditarik atau digoyang)^[2].

1. 3. Besaran Fisika pada Ayunan Bandul

1. 3. 1. Periode (T)

Benda yang bergerak harmonis sederhana pada ayunan sederhana memiliki periode^[3]. Periode ayunan (T) adalah waktu yang diperlukan benda untuk melakukan satu getaran. Benda dikatakan melakukan satu getaran jika benda bergerak dari titik di mana benda tersebut mulai bergerak dan kembali lagi ke titik tersebut. Satuan periode adalah sekon atau detik^[3].

1. 3. 2. Frekuensi (f)

Frekuensi adalah banyaknya getaran yang dilakukan oleh benda selama satu detik, yang dimaksudkan dengan getaran di sini adalah getaran lengkap^[3]. Satuan frekuensi adalah hertz^[3].

1. 3. 3. Hubungan antara Periode dan Frekuensi

Frekuensi adalah banyaknya getaran yang terjadi selama satu detik. Dengan demikian selang waktu yang dibutuhkan untuk melakukan satu getaran adalah^[3] :

Selang waktu yang dibutuhkan untuk melakukan satu getaran adalah periode. Dengan demikian, secara matematis hubungan antara periode dan frekuensi adalah sebagai berikut^[3] :

1. 3. 4. Amplitudo

Pada ayunan sederhana, selain periode dan frekuensi, terdapat juga amplitudo. Amplitudo adalah perpindahan maksimum dari titik kesetimbangan^[3].

2. Gaya Pemulih

Gaya pemulih dimiliki oleh setiap benda elastis yang terkena gaya sehingga benda elastis tersebut berubah bentuk^[4]. Gaya yang timbul pada benda elastis untuk menarik kembali benda yang melekat padanya di sebut gaya pemulih^[4].

2. 1. Gaya Pemulih pada Pegas

Pegas adalah salah satu contoh benda elastis^[4]. Oleh sifat elastisnya ini, suatu pegas yang diberi gaya tekan atau gaya regang akan kembali pada keadaan setimbangnya mula- mula apabila gaya yang bekerja padanya dihilangkan^[4]. Gaya pemulih pada pegas banyak dimanfaatkan dalam bidang teknik dan kehidupan sehari- hari^[4]. Misalnya di dalam shockbreaker dan springbed^[4]. Sebuah pegas berfungsi meredam getaran saat roda kendaraan melewati jalan yang tidak rata^[4]. Pegas - pegas yang tersusun di dalam springbed akan memberikan kenyamanan saat orang tidur^[4].

2. 1. 1. Hukum Hooke

Robert Hooke

Jika gaya yang bekerja pada sebuah pegas dihilangkan, pegas tersebut akan kembali pada keadaan semula^[5]. Robert Hooke, ilmuwan berkebangsaan Inggris menyimpulkan bahwa sifat elastis pegas tersebut ada batasnya dan besar gaya pegas sebanding dengan pertambahan panjang pegas^[5]. Dari penelitian yang dilakukan, didapatkan bahwa besar gaya pegas pemulih sebanding dengan pertambahan panjang pegas. Secara matematis, dapat dituliskan sebagai^[5] :

, dengan k = tetapan pegas (N / m)

Tanda (-) diberikan karena arah gaya pemulih pada pegas berlawanan dengan arah gerak pegas tersebut.

2. 1. 2. Susunan Pegas

Konstanta pegas dapat berubah nilainya, apabila pegas - pegas tersebut disusun menjadi rangkaian^[5]. Besar konstanta total rangkaian pegas bergantung pada jenis rangkaian pegas, yaitu rangkaian pegas seri atau paralel^[5].

• Seri / Deret

Gaya yang bekerja pada setiap pegas adalah sebesar F, sehingga pegas akan mengalami pertambahan panjang sebesar dan . Secara umum, konstanta total pegas yang disusun seri dinyatakan dengan persamaan^[5] :

, dengan k_n = konstanta pegas ke - n.

• Paralel

Jika rangkaian pegas ditarik dengan gaya sebesar F, setiap pegas akan mengalami gaya tarik sebesar dan , pertambahan panjang sebesar dan ^[5]. Secara umum, konstanta total pegas yang dirangkai paralel dinyatakan dengan persamaan^[5] :

k_total = k₁ + k₂ + k₃ +....+ k_n, dengan k_n = konstanta pegas ke - n.

2. 2. Gaya Pemulih pada Ayunan Bandul Matematis

Ayunan Bandul Matematis

Ayunan matematis merupakan suatu partikel massa yang tergantung pada suatu titik tetap pada seutas tali, di mana massa tali dapat diabaikan dan tali tidak dapat bertambah panjang^[6]. Dari gambar tersebut, terdapat sebuah beban bermassa tergantung pada seutas kawat halus sepanjang dan massanya dapat diabaikan. Apabila bandul itu bergerak vertikal dengan membentuk sudut , gaya pemulih bandul tersebut adalah ^[6]. Secara matematis dapat dituliskan^[6] :

Oleh karena , maka :

3. Persamaan, Kecepatan, dan Percepatan Gerak Harmonik Sederhana

3. 1. Persamaan Gerak Harmonik Sederhana

Persamaan Gerak Harmonik Sederhana adalah^[6] :

Keterangan :

Y = simpangan

A = simpangan maksimum (amplitudo)

F = frekuensi

t = waktu

Jika posisi sudut awal adalah , maka persamaan gerak harmonik sederhana menjadi ^[6]:

3. 2. Kecepatan Gerak Harmonik Sederhana

Dari persamaan gerak harmonik sederhana

Kecepatan gerak harmonik sederhana^[6] :

Kecepatan maksimum diperoleh jika nilai atau , sehingga :

3. 3. Kecepatan untuk Berbagai Simpangan

Persamaan tersebut dikuadratkan

, maka^[6] :

...(1)

Dari persamaan :

...(2)

Persamaan (1) dan (2) dikalikan, sehingga didapatkan :

Keterangan :

v =kecepatan benda pada simpangan tertentu

= kecepatan sudut

A = amplitudo

Y = simpangan

3. 4. Percepatan Gerak Harmonik Sederhana

Dari persamaan kecepatan : , maka^[6] :

Percepatan maksimum jika atau = 90⁰ =

Keterangan :

a maks = percepatan maksimum

A = amplitudo

= kecepatan sudut

4. Hubungan Gerak Harmonik Sederhana (GHS) dan Gerak Melingkar Beraturan (GMB)

Gerak Melingkar

Gerak Melingkar Beraturan dapat dipandang sebagai gabungan dua gerak harmonik sederhana yang saling tegak lurus, memiliki Amplitudo (A) dan frekuensi yang sama namun memiliki beda fase relatif atau kita dapat memandang Gerak Harmonik Sederhana sebagai suatu komponen Gerak Melingkar Beraturan^[7]. Jadi dapat diimpulkan bahwa pada suatu garis lurus, proyeksi sebuah benda yang melakukan Gerak Melingkar Beraturan merupakan Gerak Harmonik Sederhana^[7]. Frekuensi dan periode Gerak Melingkar Beraturan sama dengan Frekuensi dan periode Gerak Harmonik Sederhana yang diproyeksikan^[7].

Misalnya sebuah benda bergerak dengan laju tetap (v) pada sebuah lingkaran yang memiliki jari-jari A sebagaimana tampak pada gambar di samping^[7]. Benda melakukan Gerak Melingkar Beraturan, sehingga kecepatan sudutnya bernilai konstan^[7]. Hubungan antara kecepatan linear dengan kecepatan sudut dalam Gerak Melingkar Beraturan dinyatakan dengan persamaan^[7] :

Karena jari-jari (r) pada Gerak Melingkar Beraturan di atas adalah A, maka persamaan ini diubah menjadi :

, ... (1)

Simpangan sudut (teta) adalah perbandingan antara jarak linear x dengan jari-jari lingkaran (r), dan dinyatakan dengan persamaan :

... (2), x adalah jarak linear, v adalah kecepatan linear dan t adalah waktu tempuh (x = vt adalah persamaan Gerak Lurus alias Gerak Linear). Kemudian v pada persamaan 2 digantikan dengan v pada persamaan 1 dan jari-jari r digantikan dengan A :

Dengan demikian, simpangan sudut benda relatif terhadap sumbu x dinyatakan dengan persamaan :

... (3) ( adalah simpangan waktu pada t = 0})

Pada gambar di atas, posisi benda pada sumbu x dinyatakan dengan persamaan :

...(4)

Persamaan posisi benda pada sumbu y :

Keterangan :

A = amplitudo

= kecepatan sudut

= simpangan udut pada saat t = 0

5. Aplikasi Gerak Harmonik Sederhana

5. 1. Shockabsorber pada Mobil

Shockabsorber pada mobil

Peredam kejut (shockabsorber) pada mobil memiliki komponen pada bagian atasnya terhubung dengan piston dan dipasangkan dengan rangka kendaraan^[8]. Bagian bawahnya, terpasang dengan silinder bagian bawah yang dipasangkan dengan as roda^[8]. Fluida kental menyebabkan gaya redaman yang bergantung pada kecepatan relatif dari kedua ujung unit tersebut^[8]. Hal ini membantu untuk mengendalikan guncangan pada roda^[8].

5. 2. Jam Mekanik

Jam mekanik

Roda keseimbangan dari suatu jam mekanik memiliki komponen pegas^[8]. Pegas akan memberikan suatu torsi pemulih yang sebanding dengan perpindahan sudut dan posisi kesetimbangan^[8]. Gerak ini dinamakan Gerak Harmonik Sederhana sudut (angular)^[8].

5. 3. Garpu Tala

Garpu tala

Garpu tala dengan ukuran yang berbeda menghasilkan bunyi dengan pola titinada yang berbeda^[8]. Makin kecil massa m pada gigi garpu tala, makin tinggi frekuensi osilasi dan makin tinggi pola titinada dari bunyi yang dihasilkan garpu tala^[8].

B.Gelombang Berjalan

Amplitudo pada tali yang digetarkan terus menerus akan selalu tetap, oleh karenanya gelombang yang memiliki amplitudo yang tetap setiap saat disebut gelombang berjalan.
Misalkan seutas tali kita getarkan ke atas dan ke bawah berulang-ulang seperti pada Gambar disamping ini. Titik P berjarak x dart titik 0 (sumber getar), Ketika titik 0 bergetar maka getaran tersebut merambat hingga ke titik P,Waktu yang diperlukan oleh gelombang untuk merambat dari titik o ke titik P adalah x / v dengan demikian bila titik 0 telah bergetar selama t detik maka titik p telah bergetar selama tP dengan

t_p= t- x/v

Berdasarkan uraian diatas maka akan didapatkan persamaan simpangan gelombang, sebagai berikut:
y=A sin⁡ 2π/T t

Persamaan simpangan di titik P dapat diperoleh dengan mengganti nilai t dengan tp sehingga kita dapatkan hubungan berikut.

y_p = A sin⁡ 2π/T (t- x/v)

A = amplitudo gelombang (m)
T = periode gelombang (s)
t = lamanya titik 0 (sumber getar) bergetar (s)
x = jarak titik P dari sumber getar (m)
v = cepat rambat gelombang (m/s)
yp= simpangan di titik P (m)

dalam hal ini gelombang memiliki dua kemungkinan dalam arah rambatannya, oleh karenanya perlu diperhatikan langkah sebagai berikut:

• Apabila gelombang merambat ke kanan dan titik asal 0 bergetar ke atas maka persamaan simpangan titik P yang digunakan adalah:
  
  

y_p = A sin⁡2π/T (t- x/v)

• Apabila gelombang merambat ke kiri dan titik asal 0 bergetar ke bawah maka persamaan simpangan titik P yang digunakan adalah:
  

y_p = - A sin⁡ 2π/T (t- x/v)

'

Fase di definisikan sebagai perbandingan antara waktu sesaat untuk meninggalkan titik keseimbang (titik 0) dan periode. Dengan demikian fase gelombang dititik P dapat ditulis sebagai berikut:

φ= t_p/T
= (t- x/v)/T φ_p = t/T - x/λ
= t/T- x/vT

Sehingga dihasilkan :
Sedangkan untuk mengukur besarnya sudut fase di titik P dapat dituliskan sebagai berikut:

θp = 2π φ_p
=2π (t/T- x/λ)

Beda fase antara dua titik yang berjarak X₂ dan X₁ dari sumber getar dapat dituliskan sebagai berikut:

Δφ = ( x₂ - x₁)/λ
Δφ = ∆x/λ

Nilai kecepatan dan percepatan gelombang di suatu titik dapat diketahui dengan menurunkan persamaan keduanya, sebagai berikut:

v_p = 2π/T A cos⁡ 2π/T (t- x/v)

ap= - (4π²)/T² A cos⁡ 2π/T (t- x/v)

Keterangan:
vp = kecepatan partikel di titik p (m/s)
ap = percepatan partikel di titik p (m/s2)

'Contoh soal:
Suatu gelombang berjalan memiliki persamaan y = 10 sin (0,8πt - 0,5;t) dengan y dalam cm dan t dalam detik. Tentukanlah kecepatan dan percepatan maksimumnya!
Pembahasan:
y=10sin⁡(0,8 πt-0,5 πx)
v = dy/dt
v=(10)(0,8 π) cos⁡ (0,8 πt-0,5 πx)
nilai v maksimum bila cos⁡ (0,8 πt-0,5 πx)=1

C. Gelombang Stasioner

Adalah gelombang yang memiliki amplitudo yang berubah – ubah antara nol sampai nilai maksimum tertentu.
Gelombang stasioner dibagi menjadi dua, yaitu gelombang stasioner akibat pemantulan pada ujung terikat dan gelombang stasioner pada ujung bebas.

Seutas tali yang panjangnya l kita ikat ujungnya pada satu tiang sementara ujung lainnya kita biarkan, setela itu kita goyang ujung yang bebas itu keatas dan kebawah berulang – ulang. Saat tali di gerakkan maka gelombang akan merambat dari ujung yang bebas menuju ujung yang terikat, gelombang ini disebut sebagai gelombang dating. Ketika gelombang dating tiba diujung yang terikat maka gelombang ini akan dipantulkan sehingga terjadi interferensi gelombang.
Untuk menghitung waktu yang diperlukan gelombang untuk merambat dari titik 0 ke titik P adalah (l- x)/v . sementara itu waktu yang diperlukan gelombang untuk merambat dari titik 0 menuju titik P setelah gelombang mengalami pemantulan adalah(l+x)/v , kita dapat mengambil persamaan dari gelombang dating dan gelombang pantul sebagai berikut:

y₁= A sin 2π/T (t- (l-x)/v) untuk gelombang datang,

y₂= A sin 2π/T (t- (l+x)/v+ 180⁰) untuk gelombang pantul

Keterangan:
a. Gambar pemantulan gelombang pada ujung tali yang terikat.
b. Gambar pemantulan gelombang pada ujung tali yang dapat bergerak bebas.

sehingga untuk hasil interferensi gelombang datang dan gelombang pantul di titik P yang berjarak x dari ujung terikat adalah sebagai berikut:

y = y₁+ y₂
=A sin⁡ 2π (t/T- (l-x)/λ)+ A sin⁡2π(t/T- (1+x)/λ+ 180⁰ )
Dengan menggunakan aturan sinus maka penyederhanaan rumus menjadi:
sin⁡ A + sin⁡ B = 2 sin⁡ 1/2 (A+B) - cos⁡1/2 (A-B)

Menjadi:
y= 2 A sin⁡ (2π x/λ ) cos ⁡2π (t/T - l/λ)
y= 2 A sin⁡ kx cos⁡ (2π/T t - 2πl/λ)

Rumus interferensi

y= 2 A sin⁡ kx cos⁡ (ωt- 2πl/λ)

Keterangan :
A = amplitude gelombang datang atau pantul (m)
k = 2π/λ
ω = 2π/T (rad/s)
l = panjang tali (m)
x = letak titik terjadinya interferensi dari ujung terikat (m)
λ = panjang gelombang (m)
t = waktu sesaat (s)
Ap = besar amplitude gelombang stasioner (AP)
Ap = 2 A sin kx
Jika kita perhatikan gambar pemantulan gelombang diatas , gelombang yang terbentuk adalah gelombang transversal yang memiliki bagian – bagian diantaranya perut dan simpul gelombang. Perut gelombang terjadi saat amplitudonya maksimum sedangkan simpul gelombang terjadi saat amplitudonya minimum. Dengan demikian kita akan dapat mencari letak titik yang merupakan tempat terjadinya perut atau simpul gelombang.

Tempat simpul (S) dari ujung pemantulan
S=0,1/2 λ,λ,3/2 λ,2λ,dan seterusnya
=n (1/2 λ),dengan n=0,1,2,3,….

Tempat perut (P) dari ujung pemantulan
P= 1/4 λ,3/4 λ,5/4 λ,7/4 λ,dan seterusnya
=(2n-1)[1/4 λ],dengan n=1,2,3,….

Superposisi gelombang

Jika ada dua gelombang yang merambat pada medium yang sama, gelombang-gelombang tersebut akan dating di suatu titik pada saat yang sama sehingga terjadilah superposisi gelombang . Artinya, simpangan gelombang – gelombang tersebut disetiap titik dapat dijumlahkan sehingga menghasilkan sebuah gelombang baru.
Persamaan superposisi dua gelombang tersebut dapat diturunkan sebagai berikut:
y₁ = A sin⁡ ωt ; y₂ = A sin⁡ (ωt+ ∆θ)
Kedua gelombang tersebut memiliki perbedaan sudut fase sebesar Δθ
Persamaan simpangan gelombang hasil superposisi kedua gelombang tersebut adalah:

y = 2 A sin⁡ (ωt+ ∆θ/2) cos⁡(∆θ/2)

Dengan 2A cos (∆θ/2) disebut sebagai amplitude gelombang hasil superposisi.
Dengan 2A cos (∆θ/2) disebut sebagai amplitude gelombang hasil superposisi.

D.GELOMBANG BUNYI

Bunyi

Efek Doppler menjelaskan peristiwa terjadinya perubahan frekuensi yang terdengar (fp) karena adanya gerak relatif sumber dan pendengar.

fp = fs v ± vp v ± vs

fp = frekuensi pendengar fs = frekuensi sumber v = kecepatan bunyi di udara vp = kecepatan pendengar vs = kecepatan sumber

Ketentuan :
vp Þ + ¾® pendengar mendekati sumber
0 ¾® pendengar diam
- ¾® pendengar menjauhi sumber

vs Þ + ¾® sumber mendekati pendengar
0 ¾® sumber diam
- ¾® sumber menjauhi pendengar

INTENSITAS BUNYI ( I )

v = kecepatan bunyi di udaravp = kecepatan pendengarvs = kecepatan sumber

Intensitas bunyi (I) adalah jumlah energi bunyi yang menembus tegak lurus bidang per detik.

I = P/A = P/(4pR2)	Þ I » 1/R²	P = daya bunyi (watt) A = luas bidang bole (m² atau cm²) A = 4pR² R = jarak suatu titik ke sumber bunyi
I = 2p² f² A² rv	Þ I » A²	I » f²

TARAF INTENSITAS BUNYI (TI)

TI = 10 log (I/lo)

TI mempunyai satuan desibell (dB)
Io = intensitas ambang
Io = 10E-16 watt/cm² pada frekuensi 100 Hz

Batas intensitas dan taraf intensitas yang dapat didengar pada frekuensi 1000 Hz:

10E-16 £ I £ 10E-4 watt/cm²
0 £ TI £ 120 dB

Contoh 1 :
Dua buah kawat sejenis masing-masing memiliki panjang L den 2L serta tegangan kawat F dan 4F. Jika frekuensi nada dasar dalam kawat yang pendek 60 Hz, tentukan frekuensi harmonik kedua dalam kawat yang lebih panjang !

Jawab:
f = (1/l)Ö(F/m) Þ kedua kawat sama (sejenis)

nada dasar pada kawat pendek : (syarat fo Þ L = ½ l)
fo =½ L Ö(F/m) = 60 Hz Þ F2 = 4F; L2 = 2L

nada kedua pada kawat panjang: (syarat f2 Þ L2 = 3/2l)
f2 = 3/(2 L2) Ö(F2/m) = 3/2.1/(2 L2).Ö(F/m)
f2 = 3/2.2.1/(2L) Ö(F/m) = 3.60 = 180 Hz

Contoh 2 :
Nada dasar yang dihasilkan oleh seutas dawai sama dengan nada atas kedua yang dihasilkan oleh pipa organa tertutup. Hitung perbandingan panjang pipa organa tertutup terhadap panjang dawai !

Jawab :

Dawai : fO Þ Ld = 1/2 ld ld = 2 Ld POT : f2 Þ LT = 5/4lT lT = 4/5 LT

Þ

fo = f2 v/ld = v/lT 1/(2 Ld) = 5 LT/4 LT/LD = 2×5 /4 = 5:2

Contoh 3 :
Kebisingan dari sebuah mesin tik sama dengan 70 dB. Berapa dB kebisingan suatu kantor akibat 100 buah mesin tik ?

Jawab :
Anggap intensitas satu mesin tik = I1
maka intensitas 100 mesin tik = I2 = 100 I1,

Cari penambahan kebisingan akibat 100 mesin tik :
DTI = 10 log I2/I1 = 10 log 100 I1/I1 = 20 dB
Jadi kebisingan 100 mesin tik adalah : TI2 = TI1 + DTI = 90 dB

sumber bunyi (berupa benda-benda yang bergetar) terbagi tiga, yaitu dawai (senar/tali) pipa organa terbuka dan pipa organa tertutup.

SYARAT NADA DASAR ( fo ) PIPA ORGANA TERBUKA =
NADA DASAR ( fo ) DAWAI

L = (n+1/2) l untuk fo Þ n = 0 => L = 1/2 l

SYARAT NADA DASAR PIPA ORGANA TERTUTUP

L = (2n+1) l untuk fo ® n = 0 Þ L = ¼l PERBANDINGAN FREKUENSI NADA-NADA PADA SUMBER BUNYI

Dawai	: fo : f1 : f2 = 1: 2 :3 ...
Pipa Organa Terbuka (POB)	: fo : f1 : f2 = 1 :2 :3 ...
Pipa Organa Tertutup (POT)	: fo : f1 : f2 = 1 : 3 : 5 ...

Catatan : - pada dawai, bagian yang dijepit/ditekan selalu timbul
simpul (s) gelombang. Jadi p <>.
- pada pipa organa, bagian terbuka selalu timbul perut (p)
gelombang sedangkan bagian terlutup selalu timbul simpul
(s) gelombang. Jadi p > s (POB) ; p = s (POT)
- f1 disebut nada atas 1 f2 disebut nada atas 2 dst


DISPERSI CAHAYA

Gelombang dan sifat-sifatnya sebagian sudah dikenal pada waktu membahas getaran dan gelombang. Pada bagian ini, kita akan membahas gelombang cahaya. Cahaya merupakan radiasi gelombang elektromagnetik yang dapat dideteksi mata manusia. Cahaya selain memiliki sifat-sifat gelombang secara umum misal dispersi, interferensi, difraksi, dan polarisasi, juga memiliki sifat-sifat gelombang elektromagnetik, yaitu dapat merambat melalui ruang hampa.

Gejala dispersi cahaya adalah gejala peruraian cahaya putih (polikromatik) menjadi cahaya berwarna-warni (monokromatik). Cahaya putih merupakan cahaya polikromatik, artinya cahaya yang terdiri atas banyak warna dan panjang gelombang. Jika cahaya putih diarahkan ke prisma, maka cahaya putih akan terurai menjadi cahaya merah, jingga, kuning, hijau, biru, nila, dan ungu. Cahaya-cahaya ini memiliki panjang gelombang yang berbeda. Setiap panjang gelombang memiliki indeks bias yang berbeda. Semakin kecil panjang gelombangnya semakin besar indeks biasnya. Disperi pada prisma terjadi karena adanya perbedaan indeks bias kaca setiap warna cahaya. Perhatikan Gambar 2.1.

Gambar 2.1. Dispersi cahaya pada prisma

Seberkas cahaya polikromatik diarahkan ke prisma. Cahaya tersebut kemudian terurai menjadi cahaya merah, jingga, kuning, hijau, biru, nila, dan ungu. Tiap-tiap cahaya mempunyai sudut deviasi yang berbeda. Selisih antara sudut deviasi untuk cahaya ungu dan merah disebut sudut dispersi. Besar sudut dispersi dapat dituliskan sebagai berikut:

Φ = δ_u - δ_m = (n_u – n_m) β .......................................2.1

Keterangan: Φ = sudut dispersi n_u = indeks bias sinar ungu n_m = indeks bias sinar merah δ_u = deviasi sinar ungu δ_m=deviasi sinar merah Penerapan Dispersi:

Contoh peristiwa dispersi pada kehidupan sehari-hari adalah pelangi. Pelangi hanya dapat kita lihat apbila kita membelakangi matahari dan hujan terjadi di depan kita. Jika seberkas cahaya matahari mengenai titik-titik air yang besar, maka sinar itu dibiaskan oleh bagian depan permukaan air. Pada saat sinar memasuki titik air, sebagian sinar akan dipantulkan oleh bagian belakang permukaan air, kemudian mengenai permukaan depan, dan akhirnya dibiaskan oleh permukaan depan. Karena dibiaskan, maka sinar ini pun diuraikan menjadi pektrum matahari.Peristiwa inilah yang kita lihat di langit dan disebut pelangi. Bagan terjadinya proses pelangi dapat dilihat pada Gambar 2.2.

Gambar 2.2. Proses terjadi pelangi

DIFRAKSI DAN INTERFERENSI

Difraksi

Difraksi

Prinsip Huygens.

Difraksi

Difraksi cahaya diterangkangkan oleh prinsip Huygens.

Difraksi pada dua celah berjarak d. Fraksi gelombang putih terjadi pada perpotongan antara garis-garis putih. Fraksi gelombang hitam terjadi pada perpotongan garis-garis berwarna hitam. Fraksi-fraksi gelombang terpisah sejauh sudut θ dan dirunut dengan urutan n.

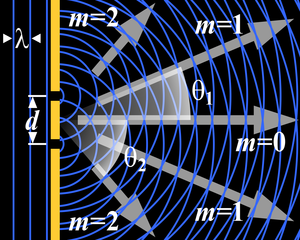
Difraksi adalah penyebaran gelombang, contohnya cahaya, karena adanya halangan. Semakin kecil halangan, penyebaran gelombang semakin besar. Hal ini bisa diterangkan oleh prinsip Huygens. Pada animasi pada gambar sebelah kanan atas terlihat adanya pola gelap dan terang, hal itu disebabkan wavelet-wavelet baru yang terbentuk di dalam celah sempit tersebut saling berinterferensi satu sama lain.

Untuk menganalisa atau mensimulasikan pola-pola tersebut, dapat digunakan Transformasi Fourier atau disebut juga dengan Fourier Optik.

Difraksi cahaya berturut-turut dipelajari antara lain oleh:

• Isaac Newton dan Robert Hooke pada tahun 1660, sebagai inflexion dari partikel cahaya yang sekarang dikenal sebagai cincin Newton.^[1]
• Francesco Maria Grimaldi pada tahun 1665 dan didefinisikan sebagai hamburan fraksi gelombang cahaya ke arah yang berbeda-beda. Istilah yang digunakan saat itu mengambil bahasa Latin diffringere yang berarti to break into pieces.^[2][3][4]
• James Gregory pada tahun 1673 dengan mengamati pola difraksi pada bulu burung^[5] yang kemudian didefinisikan sebagai diffraction grating.^[6]
• Thomas Young pada tahun 1803 dan sebagai fenomena interferensi gelombang cahaya. Dari percobaan yang mengamati pola interferensi pada dua celah kecil yang berdekatan,^[7] Thomas Young menyimpulkan bahwa kedua celah tersebut lebih merupakan dua sumber gelombang yang berbeda daripada partikel (en:corpuscles).^[8]
• Augustin Jean Fresnel pada tahun 1815^[9] dan tahun 1818^[10], dan menghasilkan perhitungan matematis yang membenarkan teori gelombang cahaya yang dikemukakan sebelumnya oleh Christiaan Huygens^[11] pada tahun 1690 hingga teori partikel Newton mendapatkan banyak sanggahan. Fresnel mendefinisikan difraksi dari eksperimen celah ganda Young sebagai interferensi gelombang^[12] dengan persamaan:

mλ = dsinθ

dimana d adalah jarak antara dua sumber muka gelombang, θ adalah sudut yang dibentuk antara fraksi muka gelombang urutan ke-m dengan sumbu normal muka gelombang fraksi mula-mula yang mempunyai urutan maksimum m = 0.^[13]. Difraksi Fresnel kemudian dikenal sebagai near-field diffraction, yaitu difraksi yang terjadi dengan nilai m relatif kecil.

• Richard C. MacLaurin pada tahun 1909, dalam monographnya yang berjudul Light^[14], menjelaskan proses perambatan gelombang cahaya yang terjadi pada difraksi Fresnel jika celah difraksi disoroti dengan sinar dari jarak jauh.
• Joseph von Fraunhofer dengan mengamati bentuk gelombang difraksi yang perubahan ukuran akibat jauhnya bidang pengamatan.^[15][16] Difraksi Fraunhofer kemudian dikenal sebagai far-field diffraction.
• Francis Weston Sears pada tahun 1948 untuk menentukan pola difraksi dengan menggunakan pendekatan matematis Fresnel^[17]. Dari jarak tegak lurus antara celah pada bidang halangan dan bidang pengamatan serta dengan mengetahui besaran panjang gelombang sinar insiden, sejumlah area yang disebut zona Fresnel (en:Fresnel zone) atau half-period elements dapat dihitung.

Difraksi Fresnel

Geometri difraksi dengan sistem koordinat antara celah pada bidang halangan dan citra pada bidang pengamatan.

Difraksi Fresnel adalah pola gelombang pada titik (x,y,z) dengan persamaan:

dimana:

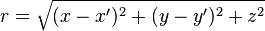, dan

is the satuan imajiner.

Difraksi Fraunhofer

Dalam teori difraksi skalar (en:scalar diffraction theory), Difraksi Fraunhofer adalah pola gelombang yang terjadi pada jarak jauh (en:far field) menurut persamaan integral difraksi Fresnel sebagai berikut:

^[18]

Persamaan di atas menunjukkan bahwa pola gelombang pada difraksi Fresnel yang skalar menjadi planar pada difraksi Fraunhofer akibat jauhnya bidang pengamatan dari bidang halangan.

Difraksi celah tunggal

Pendekatan numerik dari pola difraksi pada sebuah celah dengan lebar empat kali panjang gelombang planar insidennya.

Grafik dan citra dari sebuah difraksi celah tunggal

Sebuah celah panjang dengan lebar infinitesimal akan mendifraksi sinar cahaya insiden menjadi deretan gelombang circular, dan muka gelombang yang lepas dari celah tersebut akan berupa gelombang silinder dengan intensitas yang uniform.

Secara umum, pada sebuah gelombang planar kompleks yang monokromatik dengan panjang gelombang &lambda yang melewati celah tunggal dengan lebar d yang terletak pada bidang x′-y′, difraksi yang terjadi pada arah radial r dapat dihitung dengan persamaan:

dengan asumsi sumbu koordinaat tepat berada di tengah celah, x′ akan bernilai dari hingga 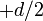, dan y′ dari 0 hingga .

Jarak r dari celah berupa:

Sebuah celah dengan lebar melebihi panjang gelombang akan mempunyai banyak sumber titik (en:point source) yang tersebar merata sepanjang lebar celah. Cahaya difraksi pada sudut tertentu adalah hasil interferensi dari setiap sumber titik dan jika fasa relatif dari interferensi ini bervariasi lebih dari 2π, maka akan terlihat minima dan maksima pada cahaya difraksi tersebut. Maksima dan minima adalah hasil interferensi gelombang konstruktif dan destruktif pada interferensi maksimal.

Difraksi Fresnel/difraksi jarak pendek yang terjadi pada celah dengan lebar empat kali panjang gelombang, cahaya dari sumber titik pada ujung atas celah akan berinterferensi destruktif dengan sumber titik yang berada di tengah celah. Jarak antara dua sumber titik tersebut adalah λ / 2. Deduksi persamaan dari pengamatan jarak antara tiap sumber titik destruktif adalah:

Minima pertama yang terjadi pada sudut &theta minimum adalah:

Difraksi jarak jauh untuk pengamatan ini dapat dihitung berdasarkan persamaan integral difraksi Fraunhofer menjadi:

dimana fungsi sinc berupa sinc(x) = sin(px)/(px) if x ? 0, and sinc(0) = 1.

Difraksi celah ganda

Sketsa interferensi Thomas Young pada difraksi celah ganda yang diamati pada gelombang air.^[19]

Pada mekanika kuantum, eksperimen celah ganda yang dilakukan oleh Thomas Young menunjukkan sifat yang tidak terpisahkan dari cahaya sebagai gelombang dan partikel. Sebuah sumber cahaya koheren yang menyinari bidang halangan dengan dua celah akan membentuk pola interferensi gelombang berupa pita cahaya yang terang dan gelap pada bidang pengamatan, walaupun demikian, pada bidang pengamatan, cahaya ditemukan terserap sebagai partikel diskrit yang disebut foton.^[20][21]

Pita cahaya yang terang pada bidang pengamatan terjadi karena interferensi konstruktif, saat puncak gelombang (en:crest) berinterferensi dengan puncak gelombang yang lain, dan membentuk maksima. Pita cahaya yang gelap terjadi saat puncak gelombang berinterferensi dengan landasan gelombang (en:trough) dan menjadi minima. Interferensi konstruktif terjadi saat:

dimana

λ adalah panjang gelombang cahaya

a adalah jarak antar celah, jarak antara titik A dan B pada diagram di samping kanan

n is the order of maximum observed (central maximum is n = 0),

x adalah jarak antara pita cahaya dan central maximum (disebut juga fringe distance) pada bidang pengamatan

L adalah jarak antara celah dengan titik tengah bidang pengamatan

Persamaan ini adalah pendekatan untuk kondisi tertentu.^[22] Persamaan matematika yang lebih rinci dari interferensi celah ganda dalam konteks mekanika kuantum dijelaskan pada dualitas Englert-Greenberger.

Difraksi celah majemuk

Difraksi celah ganda (atas) dan difraksi celah 5 dari sinar laser

Difraksi sinar laser pada celah majemuk

Pola difraksi dari sinar laser dengan panjang gelombang 633 nm laser melalui 150 celah

Diagram dari difraksi dengan jarak antar celah setara setengah panjang gelombang yang menyebabkan interferensi destruktif

Difraksi celah majemuk (en:Diffraction grating) secara matematis dapat dilihat sebagai interferensi banyak titik sumber cahaya, pada kondisi yang paling sederhana, yaitu yang terjadi pada dua celah dengan pendekatan Fraunhofer, perbedaan jarak antara dua celah dapat dilihat pada bidang pengamatan sebagai berikut:

Dengan perhitungan maksima:

		dimana adalah urutan maksima adalah panjang gelombang adalah jarak antar celah and adalah sudut terjadinya interferensi konstruktif

Dan persamaan minima:

.

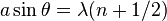Pada sinar insiden yang membentuk sudut θ_i terhadap bidang halangan, perhitungan maksima menjadi:

Cahaya yang terdifraksi dari celah majemuk dapat dihitung dengan penjumlahan difraksi yang terjadi pada setiap celah berupa konvolusi dari pola difraksi dan interferensi.

INTERFERENSI

Interferensi Cahaya

Interferensi cahaya merupakan interaksi dua atau lebih gelombang cahaya yang menghasilkan suatu intensitas radiasi yang menyimpang dari jumlah masing-masing komponen radiasi gelombangnya. Interferensi menghasilkan suatu pola interferensi terang-gelap-terang-gelap. Secara prinsip interferensi merupakan proses superposisi gelombang / cahaya. Intensitas medan di suatu titik merupakan jumlah medan-medan yang bersuperposisi.

Interferensi cahaya merupakan perpaduan atau lebih sumber cahaya sehingga menghasilkan keadaan yang lebih terang (interferensi maksimum) dan keadaan yang gelap (interferensi minimum).syarat terjadinya interferensi cahaya adalah cahaya yang koheren.

Gambar 1 gelombang dari dua sumber bersuperposisi (Hecht, 2002)

Ketika kedua gelombang yang berpadu sefase (beda fase= 0, 2?, 4?,… atau beda lintasan = 0, ?, 2?, 3?, …) terjadi interferensi konstruktif (saling menguatkan).gelombang resultan memiliki amplitude maksimum.ketika kedua gelombang yang berpadu berlawanan fase (beda fase = ?, 3?, 5?, … atau beda lintasan = 1/2?, 3/2?, 5/2?,….) terjadi inetrferensi destruktif (saling melemahkan).gelombang resultan memiliki amplitude napatkan garis nol. Interferensi yang menguatkan akan menghasilkan pola terang dan interferensi saling melemahkan akan menghasilkan pola gelap. Pada interferensi maksimum pada layar didapatkan garis terang apabila beda jalan cahaya antara celah merupakan bilangan genap dari setengah panjang gelombang, sedangakan interferensi minimum pada layar didapatkan garis gelap apabila beda jalan antara kedua berkas cahaya merupakan bilangan ganjil dari setengah panjang gelombang.

Gambar 2 interferensi konstruktif dan destruktif

• Interferensi dari Amplitudo

Interferensi ini terjadi karena gelombang cahaya atau sinar terefleksi dan terefraksi pada batas antara 2 media yang berbeda indeks biasnya. Sinar datang terefleksi dan terrefraksi komponennya dari pemisahan gelombang dan melalui perbedaan lintasan optik. Gelombang-gelombang tersebut berinterferensi ketika berkombinasi (superposisi).

Pertama kita mempertimbangkan efek interferensi yang dihasilkan dari pembagian amplitudo. Pada gambar 2.4 sebuah sinar monokromatik dengan panjang gelombang ? di udara datang dengan sudut i pada bidang paralel lempengan suatu material dengan tebal t dan indeks bias n > 1. sinar tersebut mengalami pantulan parsial dan pembiasan pada bagian atas permukaan. Sebagian pembiasan cahaya dipantulkan dari bagian permukaan bawah dan muncul paralel ke pemantulan pertama dengan beda fase ditemukan dari perbedaan panjang lintasan optis yang dilalui pada material. Sinar paralel ini bertemu dan berinterferensi pada keadaan tak terbatas tetapi mereka mungkin dibawa menuju fokus dengan lensa. Perbedaan panjang lintasan optik gelombang-gelombang ini ditunjukkan sebagai berikut

Karena sin i = n sin ?

Gambar 3

Frinji interferensi dihasilkan pada kondisi tak terbatas dari pembagian amplitudo ketika tebal material konstan. Frinji orde ke-m adalah lingkaran terpusat dari sumber S dan terjadi untuk ?? konstan pada 2nt cos ? =?(m + 1/2) ?.

Ketika ketebalan t tidak konstan dan muka lempengan, gambar 2.6 a dan b, sinar interferensi tidak paralel namun bertemu pada titik (nyata atau maya) dekat dengan baji.Resultan interferensi frinji terbentuk dekat dengan baji dan hampir paralel dengan lapisan tipis bagian akhir dari baji. Ketika observasi dibuat pada normal dari baji cos q ~ 1 dan berubah perlahan pada daerah ini sehingga 2nt cos q » 2nt. Kondisi ini untuk pola frinji terang lalu perumusannya menjadi:

2nt = (m + 1/2) ? [1]

Dan setiap frinji meletakkan nilai khusus dari ketebalan t dan ini memberikan pola frinji. Seperti nilai m berubah menjadi m+1, ketebalan berubah dengan kelipatan ?/2n dan frinji memungkinkan pengukuran panjang gelombang dari cahaya.

Polarisasi Cahaya

Polarisasi adalah peristiwa penyerapan arah bidang getar dari gelombang. Gejala polarisasi hanya dapat dialami oleh gelombang transversal saja, sedangkan gelombang longitudinal tidak mengalami gejala polarisasi. Fakta bahwa cahaya dapat mengalami polarisasi menunjukkan bahwa cahaya merupakan gelombang transversal.

Pada umumnya, gelombang cahaya mempunyai banyak arah getar. Suatu gelombang yang mempunyai banyak arah getar disebut gelombang tak terpolarisasi, sedangkangelombang yang memilki satu arah getar disebut gelombang terpolarisasi.

Gejala polarisasi dapat digambarkan dengan gelombang yang terjadi pada tali yang dilewatkan pada celah. Apabila tali digetarkan searah dengan celah maka gelombang pada tali dapat melewati celah tersebut. Sebaliknya jika tali digetarkan dengan arah tegak lurus celah maka gelombang pada tali tidak bisa melewati celah tersebut.

Sinar alami seperti sinar Matahari pada umumnya adalah sinar yang tak terpolarisasi. Sinar tak terpolarisasi dilambangkan sedangkan sinar yang terpolarisasi dilambangkan atau . Cahaya dapat mengalami polarisasi dengan berbagai cara, antara lain karena peristiwa pemantulan, pembiasan, bias kembar, absorbsi selektif, dan hamburan.

1. Polarisasi karena Pemantulan

Cahaya yang datang ke cermin dengan sudut datang sebesar 57o, maka sinar yang terpantul akan merupakan cahaya yang terpolarisasi. Cahaya yang berasal dari cermin I adalah cahaya terpolarisasi akan dipantulkan ke cermin.

Apabila cermin II diputar sehingga arah bidang getar antara cermin I dan cermin II saling tegak lurus, maka tidak akan ada cahaya yang dipantulkan oleh cermin II. Peristiwa ini menunjukkan terjadinya peristiwa polarisasi. Cermin I disebut polarisator, sedangkan cermin II disebut analisator. Polarisator akan menyebabkan sinar yang tak terpolarisasi menjadi sinar yang terpolarisasi, sedangkan

2. Polarisasi karena Pemantulan dan Pembiasan

Berdasarkan hasil eksperimen yang dilakukan para ilmuwan Fisika menunjukkan bahwa polarisasi karena pemantulan dan pembiasan dapat terjadi apabila cahaya yang dipantulkan dengan cahaya yang dibiaskan saling tegak lurus atau membentuk sudut 90o.

Di mana cahaya yang dipantulkan merupakan cahaya yang terpolarisasi sempurna, sedangkan sinar bias merupakan sinar terpolarisasi sebagian. Sudut datang sinar yang dapat menimbulkan cahaya yang dipantulkan dengan cahaya yang dibiaskan merupakan sinar yang terpolarisasi.

Sudut datang seperti ini dinamakan sudut polarisasi (ip) atau sudut Brewster. Pada saat sinar pantul dan sinar bias saling tegak lurus (membentuk sudut 90o) akan berlaku ketentuan bahwa : iw + r = 90o atau r = 90o - i

3. Polarisasi karena Bias Kembar (Pembiasan Ganda)

Polarisasi karena bias kembar dapat terjadi apabila cahaya melewati suatu bahan yang mempunyai indeks bias ganda atau lebih dari satu, misalnya pada kristal kalsit.

Cahaya yang lurus disebut cahaya biasa, yang memenuhi hukum Snellius dan cahaya ini tidak terpolarisasi. Sedangkan cahaya yang dibelokkan disebut cahaya istimewa karena tidak memenuhi hukum Snellius dan cahaya ini adalah cahaya yang terpolarisasi.

4. Polarisasi karena Absorbsi

Selektif Polaroid adalah suatu bahan yang dapat menyerap arah bidang getar gelombang cahaya dan hanya melewatkan salah satu bidang getar. Seberkas sinar yang telah melewati polaroid hanya akan memiliki satu bidang getar saja sehingga sinar yang telah melewati polaroid adalah sinar yang terpolarisasi.

Peristiwa polarisasi ini disebut polarisasi karena absorbsi selektif. Polaroid banyak digunakan dalam kehidupan sehari-hari, antara lain untuk pelindung pada kacamata dari sinar matahari (kacamata sun glasses) dan polaroid untuk kamera.

5. Polarisasi karena Hamburan

Polarisasi cahaya karena peristiwa hamburan dapat terjadi pada peristiwa terhamburnya cahaya matahari oleh partikel-partikel debu di atmosfer yang menyelubungi Bumi. Cahaya matahari yang terhambur oleh partikel debu dapat terpolarisasi. Itulah sebabnya pada hari yang cerah langit kelihatan berwarna biru. Hal itu disebabkan oleh warna cahaya biru dihamburkan paling efektif dibandingkan dengan cahaya-cahaya warna yang lainnya.

6. Pemutaran Bidang Polarisasi

Seberkas cahaya tak terpolarisasi melewati sebuah polarisator sehingga cahaya yang diteruskan terpolarisasi. Cahaya terpolarisasi melewati zat optik aktif, misalnya larutan gula pasir, maka arah polarisasinya dapat berputar. Besarnya sudut perubahan arah polarisasi cahaya


Gaya Lorentz

Jika arus listrik mengalir dari A ke B ternyata pita dari alumunium foil melengkung ke atas , ini berarti ada sesuatu gaya yang berarah keatas akibat adanya medan magnet homogen dari utara ke selatan. Gaya ini selanjutnya disebut sebagai gaya magnetic atau gaya Lorentz . Jika arus listrik dibalik sehingga mengalir dari B ke A, ternyata pita dari alumunium foil melengkung ke bawah. Jika arus listrik diperbesar maka alumunium foil akan melengkung lebih besar. Ini berarti besar dan arah gaya Lorentz tergantung besar dan arah arus listrik.
Karena gaya Lorentz ( FL ) , arus listrik ( I ) dan medan magnet ( B ) adalah besaran vector maka peninjauan secara matematik besar dan arah gaya Lorentz ini hasil perkalian vector ( cros-product ) dari I dan B.

FL = I x B

Besarnya gaya Lorentz dapat dihitung dengan rumus FL = I.B sinθ
Rumus ini berlaku untuk panjang kawat 1 meter.

Perhitungan diatas adalah gaya Lorentz yang mempengaruhi kawat tiap satuan panjang. Jadi jika panjang kawat = ℓ , maka besar gaya Lorentz dapat dihitung dengan rumus :

FL = I . ℓ . B . Sin θ

• FL = gaya Lorentz dalam newton ( N )
• I = kuat arus listrik dalam ampere ( A )
• ℓ = panjang kawat dalam meter ( m )
• B = kuat medan magnet dalam Wb/m² atau tesla ( T )
• θ = sudut antara arah I dan B

Dari rumus di atas ternyata jika besar sudut θ adalah :

• Θ =900 , arah arus listrik dan medan magnet ( I dan B ) saling tegak lurus maka FL mencapai maksimum
• Θ = 00 , arah arus listrik dan medan magnet ( I dan B ) saling sejajar maka FL = 0 atau kawat tidak dipengaruhi gaya Lorentz

Hubungan antara FL , I dan B dapat lebih mudah dipelajari dengan menggunakan kaidah tangan kiri. Yaitu dengan mengangan-angankan jika ibu jari, jari telunjuk dan jari tangah kita bentangkan saling tegak lurus, maka :

• Ibu jari : menunjukan arah gaya Lorentz ( FL ) Arah gaya Lorentz
• Jari telunjuk : menunjukkan arah medan magnet ( B )
• Jari tengah : menunjukkan arah arus listrik ( I )

Coba sekarang kalian terapkan kaidah ini pada percobaan diatas, mengapa alumunium foil melengkung keatas ? sesuaikah dengan kaidah tangan kiri ?

Catatan :
Aturan ini dapat juga menggunakan kaidah tangan kanan, yaitu dengan mengangan-angankan jika Ibu jari, Jari Telunjuk dan Jari tengah kita bentangkan saling tegak lurus, maka : Jari tengah menunjuk arah gaya Lorentz, jari telunjuk menunjuk arah medan magnet dan Ibu jari menunjuk arah arus listrik.

Contoh Soal :

1. Sebuah kawat berarus listrik I = 2 A membentang horizontal dengan arah arus dari utara ke selatan, berada dalam medan magnet homogen B = 10 – 4 T dengan arah vertikal ke atas. Bila panjang kawatnya 5 meter dan arah arus tegak lurus arah medan magnet. Berapa besar dan arah gaya Lorentz yang dialami oleh kawat ? ...

   Jawab :
   Diket : I = 2 A
   B = 10 – 4 T
   ℓ = 5 m
   
   Ditanya : FL = ............... ?
   Dijawab :
   
   FL = I . ℓ . B . sin θ
   = 2 ampere . 5 meter . 10 ^-4 Tesla . sin 900
   = 10^-3 newton
   
   Dengan arah gaya menunjuk ke Barat

GGL INDUKSI

GGL INDUKSI

Pada bab sebelumnya, kamu sudah mengetahui bahwa kelistrikan dapat menghasilkan kemagnetan. Menurutmu, dapatkah kemagnetan menimbulkan kelistrikan? Kemagnetan dan kelistrikan merupakan dua gejala alam yang prosesnya dapat dibolak-balik. Ketika H.C. Oersted membuktikan bahwa di sekitar kawat berarus listrik terdapat medan magnet (artinya listrik menimbulkan magnet), para ilmuwan mulai berpikir keterkaitan antara kelistrikan dan kemagnetan. Tahun 1821 Michael Faraday membuktikan bahwa perubahan medan magnet dapat menimbulkan arus listrik (artinya magnet menimbulkan listrik) melalui eksperimen yang sangat sederhana. Sebuah magnet yang digerakkan masuk dan keluar pada kumparan dapat menghasilkan arus listrik pada kumparan itu. Galvanometer merupakan alat yang dapat digunakan untuk mengetahui ada tidaknya arus listrik yang mengalir. Ketika sebuah magnet yang digerakkan masuk dan keluar pada kumparan (seperti kegiatan di atas), jarum galvanometer menyimpang ke kanan dan ke kiri. Bergeraknya jarum galvanometer menunjukkan bahwa magnet yang digerakkan keluar dan masuk pada kumparan menimbulkan arus listrik. Arus listrik bisa terjadi jika pada ujung-ujung kumparan terdapat GGL (gaya gerak listrik). GGL yang terjadi di ujung-ujung kumparan dinamakan GGL induksi. Arus listrik hanya timbul pada saat magnet bergerak. Jika magnet diam di dalam kumparan, di ujung kumparan tidak terjadi arus listrik.

1. Penyebab Terjadinya GGL Induksi

Ketika kutub utara magnet batang digerakkan masuk ke dalam kumparan, jumlah garis gaya-gaya magnet yang terdapat di dalam kumparan bertambah banyak. Bertambahnya jumlah garis- garis gaya ini menimbulkan GGL induksi pada ujung-ujung kumparan. GGL induksi yang ditimbulkan menyebabkan arus listrik mengalir menggerakkan jarum galvanometer. Arah arus induksi dapat ditentukan dengan cara memerhatikan arah medan magnet yang ditimbulkannya. Pada saat magnet masuk, garis gaya dalam kumparan bertambah. Akibatnya medan magnet hasil arus induksi bersifat mengurangi garis gaya itu. Dengan demikian, ujung kumparan itu merupakan kutub utara sehingga arah arus induksi seperti yang ditunjukkan Gambar 12.1.a (ingat kembali cara menentukan kutub-kutub solenoida).

Ketika kutub utara magnet batang digerakkan keluar dari dalam kumparan, jumlah garis-garis gaya magnet yang terdapat di dalam kumparan berkurang. Berkurangnya jumlah garis-garis gaya ini juga menimbulkan GGL induksi pada ujung-ujung kumparan. GGL induksi yang ditimbulkan menyebabkan arus listrik mengalir dan menggerakkan jarum galvanometer. Sama halnya ketika magnet batang masuk ke kumparan. pada saat magnet keluar garis gaya dalam kumparan berkurang. Akibatnya medan magnet hasil arus induksi bersifat menambah garis gaya itu. Dengan demikian, ujung, kumparan itu merupakan kutub selatan, sehingga arah arus induksi seperti yang ditunjukkan Gambar 12.1.b. Ketika kutub utara magnet batang diam di dalam kumparan, jumlah garis-garis gaya magnet di dalam kumparan tidak terjadi perubahan (tetap). Karena jumlah garis-garis gaya tetap, maka pada ujung-ujung kumparan tidak terjadi GGL induksi. Akibatnya, tidak terjadi arus listrik dan jarum galvanometer tidak bergerak. Jadi, GGL induksi dapat terjadi pada kedua ujung kumparan jika di dalam kumparan terjadi perubahan jumlah garis-garis gaya magnet (fluks magnetik). GGL yang timbul akibat adanya perubahan jumlah garis-garis gaya magnet dalam kumparan disebut GGL induksi. Arus listrik yang ditimbulkan GGL induksi disebut arus induksi. Peristiwa timbulnya GGL induksi dan arus induksi akibat adanya perubahan jumlah garis-garis gaya magnet disebut induksi elektromagnetik. Coba sebutkan bagaimana cara memperlakukan magnet dan kumparan agar timbul GGL induksi?

2. Faktor yang Memengaruhi Besar GGL Induksi Sebenarnya besar kecil GGL induksi dapat dilihat pada besar kecilnya penyimpangan sudut jarum galvanometer. Jika sudut penyimpangan jarum galvanometer besar, GGL induksi dan arus induksi yang dihasilkan besar. Bagaimanakah cara memperbesar GGL induksi? Ada tiga faktor yang memengaruhi GGL induksi, yaitu : a. kecepatan gerakan magnet atau kecepatan perubahan jumlah garis-garis gaya magnet (fluks magnetik), b. jumlah lilitan, c. medan magnet